2. Základní pojmy / Vzdálenost / metrika
Ohodnocení hran
Již v úvodu k teorii grafů jsme si ukázali, že hrany k sobě mohou mít přiřazené číslo, které si lze představit jako vzdálenost mezi městy nebo např. cenu, kterou musíme zaplatit za průchod hranou. Říkáme, že graf má ohodnocené hrany.
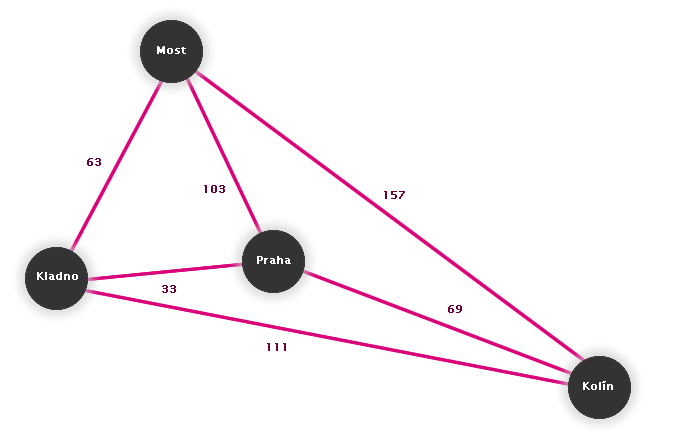
Obr. č. 2.28 - Znázornění vzdáleností mezi městy pomocí grafu
Definice ohodnocení
Funkci, která k hranám přiřadí čísla (budeme pro jednoduchost pracovat s kladnými reálnými čísly) nazveme ohodnocením hran a označíme ji w.
w: E(G) → (0, +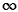
)
Grafová vzdálenost / metrika
Úvod
Pokud máme ohodnocené hrany, jsme schopni říct, jaká je vzdálenost mezi každými dvěma městy (reprezentovanými vrcholy). (Musíme se ovšem umět z jakéhokoliv města dostat do jiného (např. cestou přes nějaké třetí) - graf musí být souvislý.) Funkci, která nám dosadí k vrcholům nejkratší vzdálenosti, nazveme metrika.
Definice vzdálenosti v grafu
Nechť G = (V,E) je souvislý graf. Pro vrcholy v, v' definujme číslo dG(v,v') jako délku nejkratší cesty z v do v' v grafu G. Číslo dG(v,v') se nazývá vzdálenost vrcholů v a v' v grafu G.
Vlastnosti metriky
Funkce dG: V × V → R0+, kterou nazýváme metrika grafu G, má následující vlastnosti:
- dG(v,v')
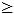0 pro každou dvojici v, v' - dG(v,v') = 0 právě tehdy, když v = v' pro každou dvojici v, v'
- dG(v,v') = dG(v',v) pro každou dvojici v, v'
- dG(v,v'')
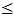dG(v,v') + dG(v',v'') pro každou trojici v, v', v''
Poslední vlastnost je tzv. trojúhelníková nerovnost - říká nám, že jsme v grafu získali vždy nejkratší vzdálenosti - pokud bychom se pokusili jít z města (vrcholu) v do v'' přes v', bude cesta stejně dlouhá nebo delší (→ v tabulce metriky známe nejkratší cesty).
Příklad metriky
Pro ukázkový graf (Obr. č. 25) by výsledek metriky vypadal následovně:
| - | Most | Kladno | Praha | Kolín |
| Most | 0 | 63 | 96 | 157 |
| Kladno | 63 | 0 | 33 | 102 |
| Praha | 96 | 33 | 0 | 69 |
| Kolín | 157 | 102 | 69 | 0 |
Poznámka: Všimněte si, že grafová vzdálenost vyšla menší než standardní (přímá) vzdálenost - algoritmus pro hledání nejkratší cesty sám správně spočítal, že např. cesta z Kladna do Kolína nemusí měřit 111km, ale 102km (33+69), pokud by cesta vedla přes Prahu.
Více informací o hledání nejkratší cesty v kapitole Vybrané problémy.