1. Úvod / Využití grafů
Co jsou grafy?
Ještě před matematickou definicí grafu je vhodné si říct, co grafy jsou a k čemu se využívají. Grafů rozeznáváme celou řadu typů, v tomto textu nám však nepůjde ani o grafy využívané ve statistice (sloupcový, koláčový...), ani o grafy funkcí.
Grafy si můžeme představit jako zjednodušení reálného světa, kde studovaný problém znázorníme pomocí bodů a čar, které je spojují, a tím popisují vlastnosti. Takovým bodům pak v teorii grafů říkáme vrcholy grafu a čáry, které je spojují, nazýváme hrany grafu.
Příklad 1: města na mapě
Jedním z typických problémů teorie grafů je hledání nejkratší cesty.
Představme si, že chceme zjistit nejkratší cestu mezi vybranými městy (pro zjednodušení jsou na obrázku č. 2.28 jen čtyři města).
Jediná vlastnost, která nás bude zajímat, je vzdálenost mezi městy (vzdálenost = délka cesty, kterou bychom museli ujet po silnici). Jako vrcholy tedy použijeme města; hrany pak budou popisovat, že mezi městy existuje cesta a jak je dlouhá. Přitom zanedbáváme další, v tuto chvíli zbytečné informace - z kolika různých silnic se cesta skládá, jakého jsou tvaru nebo například zeměpisná poloha měst (sever, jih...). Jediné informace, které pak algoritmus (zjednodušeně: postup řešení problému) využije, budou čísla na hranách spojujících města (vzdálenosti mezi městy).
Podrobněji se k této úloze vrátíme v kapitole 2.
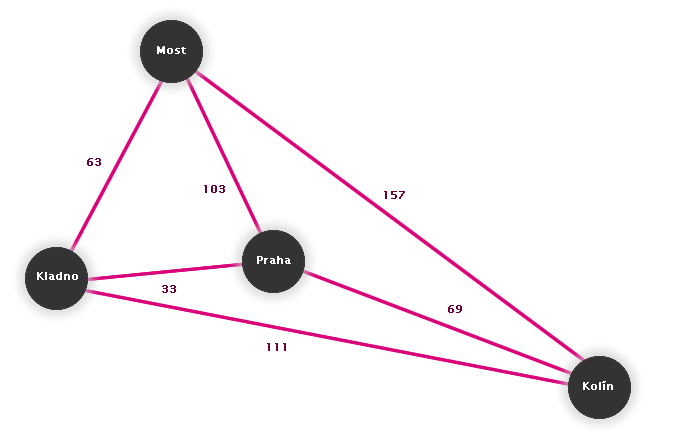
Znázornění vzdáleností mezi městy pomocí grafu - obrázek z Kapitoly 2, 2.28
Příklad 2: kamarádi
Následující problém ukazuje možnosti popisu rozličných situací pomocí grafů.
Mějme čtyři kamarády: Annu, Petra, Honzu a Václava. Pomocí grafu znázorníme, kdo koho zná (kdo s kým kamarádí). Znalostí grafů lze pak jednodušeji dokazovat různé důsledky - podobnou úlohu z matematické olympiády si můžete vyzkoušet zde.
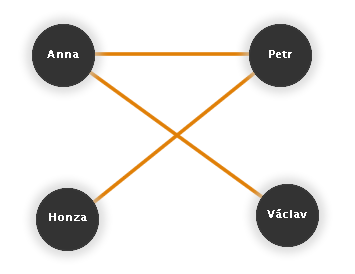
Obr. č. 1.1 - Kamarádi
Příklad 3: stromy
Stromy jsou zvláštním typem grafů často používaným v informatice (více o stromech). Pomocí vhodně navrženého stromu lze např. jednodušeji vyhledávat či třídit čísla - příklad: binární vyhledávácí strom.
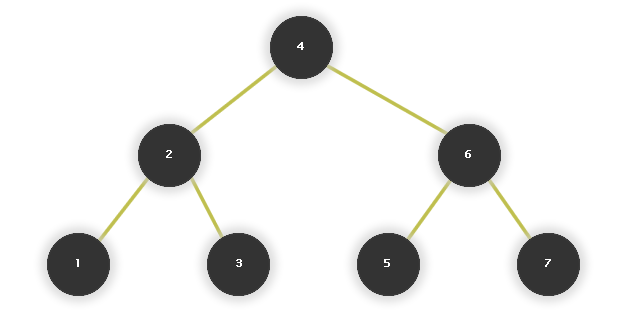
Binární vyhledávací strom - obrázek z Kapitoly 2, 2.30