3. Vybrané problémy / Alkany
Úvod
Pomocí grafů můžeme také popisovat chemické sloučeniny. Za vrcholy grafu použijeme jednotlivé atomy, hrana bude znázorňovat chemickou vazbu mezi nimi. (Pro znázornění problematiky nám postačí uvažovat pouze jednoduchou vazbu.)
Na následujícím příkladu si lze pomocí teorie grafů ukázat, proč strukturní vzroce alkanů jsou stromy.
Alkany: CnH2n+2
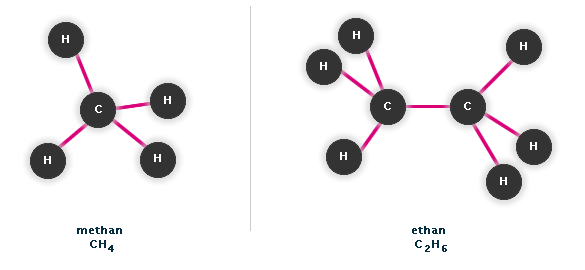
Obr. č. 3.4 - Příklady dvou nejjednoduších alkanů (methan, ethan)
Co jsou alkany?
Alkany jsou uhlovodíky neobsahující žádné násobné vazby mezi svými molekulami. Obsahuje-li molekula více než čtyři atomy uhlíku, může vznikat více izomerů (molekul se stejným souhrnným vzorcem, ale různými strukturními vzorci).
Postup
- Molekuly alkanů tvoří stromy (jsou souvislé a neobsahují cyklus).
- Pro každý strom platí Eulerův vzorec: |V| = |E| + 1
- Nyní ověříme, že graf popisující alkan se vzorcem CnH2n+2 je stromem.
- Molekuly vodíku a uhlíku znázorňujeme jako vrcholy, tzn. |V| = n + (2n + 2) = 3n + 2.
- |E| je rovno počtu vazeb. Z každé molekuly uhlíku vycházejí 4 vazby (tj. celkem 4n hran) a z každé molekuly vodíku vychází jedna hrana (tj. celkem 2n+2 hran).
- Tímto postupem jsme každou vazbu započetli dvakrát, proto musíme výsledek vydělit dvěma:
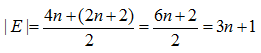
- Ukázali jsme, že alkany splňují Eulerův vzorec, tedy jejich vzorce můžeme v teorii grafů považovat za stromy.