3. Vybrané problémy / Převozník
Úvod
Pomocí teorie grafů lze řešit také populární matematickou úlohu o převozníkovi, kterou uvedl už Alkuin z Yorku (cca 735-804) ve sbírce Úlohy k bystření mladíků.
Zadání [6]
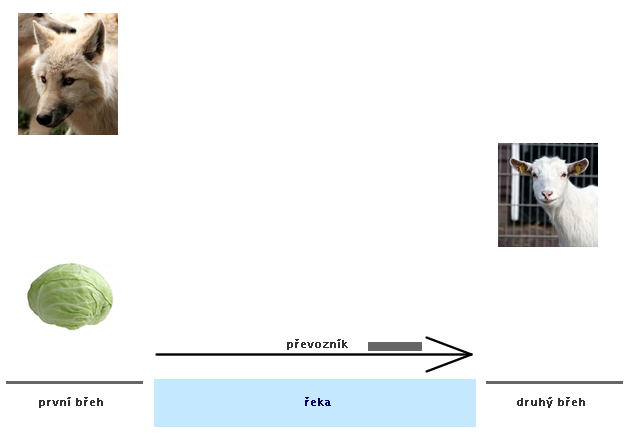
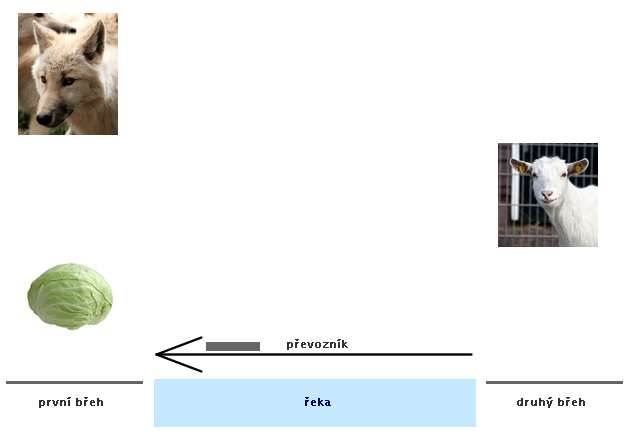
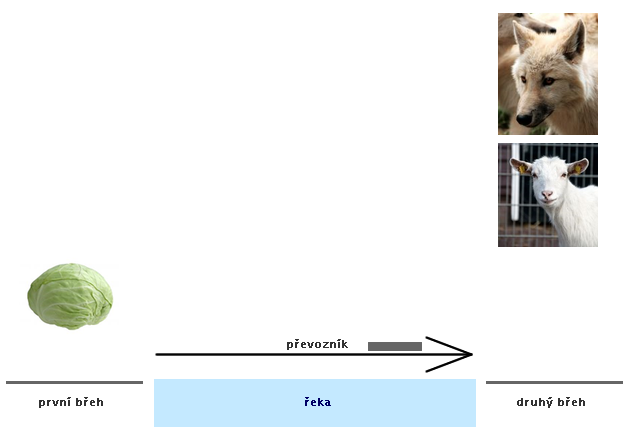
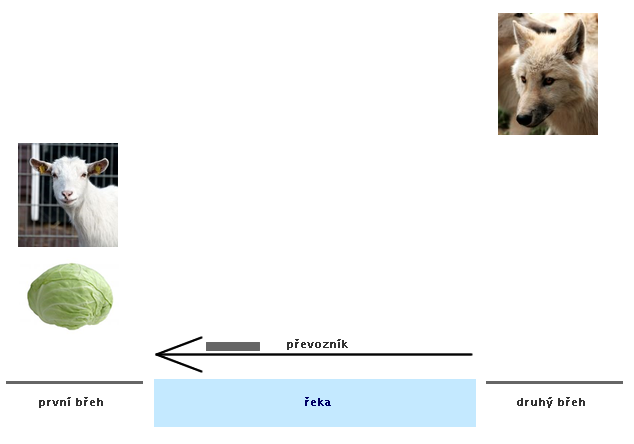
Převozník chce převézt z jednoho břehu na druhý hlávku zelí, kozu a vlka. Do loďky s sebou může vzít buď zelí, nebo kozu, nebo vlka, ale víc se tam nevejde. Nechá-li na břehu hlávku zelí a kozu, koza zelí sežere. Nechá-li na břehu kozu a vlka, pak vlk sežere kozu.
Jakým způsobem musí převozník postupovat, aby nedošlo k žádné škodě?

Obr. č. 3.22 - Ilustrace k úloze o převozníkovi
Řešení pomocí teorie grafů
Pomocí vrcholů grafu popíšeme situaci na prvním břehu. Takovýchto vrcholů (možností, kdo zůstal na prvním břehu) máme 16.
Proč 16 možností?
Máme 4 "objekty", u kterých nás zajímá, zda na břehu jsou nebo ne - vlka, zelí, převozníka a kozu.
Máme tedy dvě možnosti (je na břehu/není) pro každý ze 4 objektů - celkem 2×2×2×2 = 2^4 = 16 možností.

Obr. č. 3.23 - Znázornění situace na prvním břehu
Pomocí hran v grafu si můžeme popsat změnu, která se stala (odvezl-li převozník zelí na druhý břeh, můžeme si na hranu poznamenat "-zelí,-převozník" - z důvodu přehlednosti není popis na hranách v obrázku uveden).
Potřebujeme pospojovat vrcholy grafu tak, abychom se dostali z levého horního vrcholu (na prvním břehu jsou všichni) do pravého dolního vrcholu (na prvním břehu není nikdo).
Ne všechny vrcholy zakreslené na obrázku č. 3.23 jsou však přípustné. Nesmíme nechat bez dozoru kozu s vlkem a také kozu a zelí. Z toho důvodu celkem 6 vrcholů vypustíme.
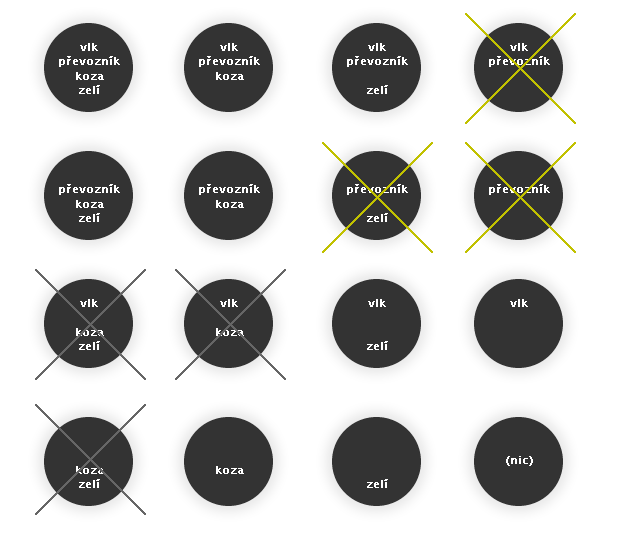
Obr. č. 3.24 - Znázornění situace na prvním břehu - jen povolené vrcholy
Pokud se vám zdá, že vrcholy přeškrtnuté žlutou barvou podmínky neporušují, vzpomeňte si, že zakreslujeme situaci na prvním břehu. Pokud jsme tedy nechali spolu vlka s převozníkem, není to v pořádku, protože na druhém břehu nám zůstala koza se zelím.
Nyní v grafu hledáme cestu (začínající v levém horním rohu a končící v pravém dolním rohu), která by popisovala při zachování předepsaných podmínek průběh přepravy. Všimněte si, že se po cestě střídají vrcholy s převozníkem a bez něho - podle toho, jak vozí ostatní z břehu na břeh. Jak vidíte, úloha má dvě možná řešení.
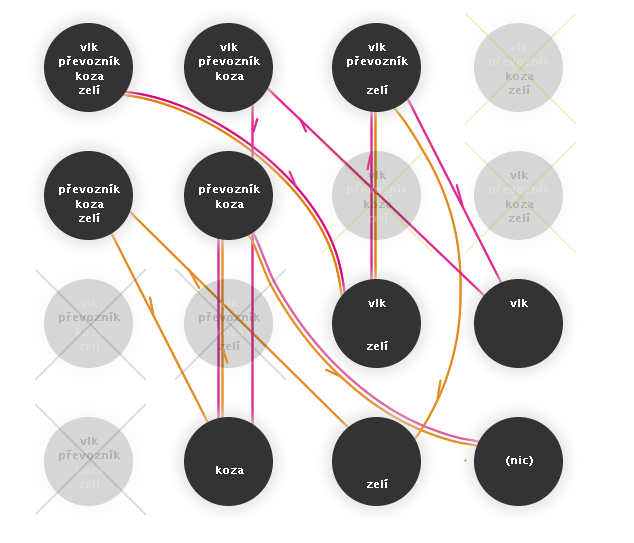
Obr. č. 3.25 - Řešení úlohy
Řešení č. 1 - fialové hrany (animace)

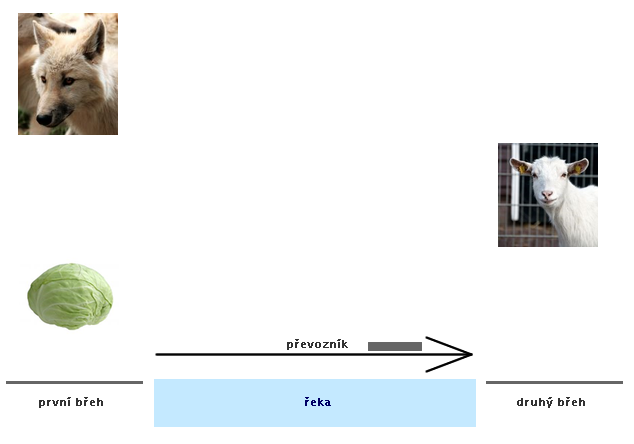
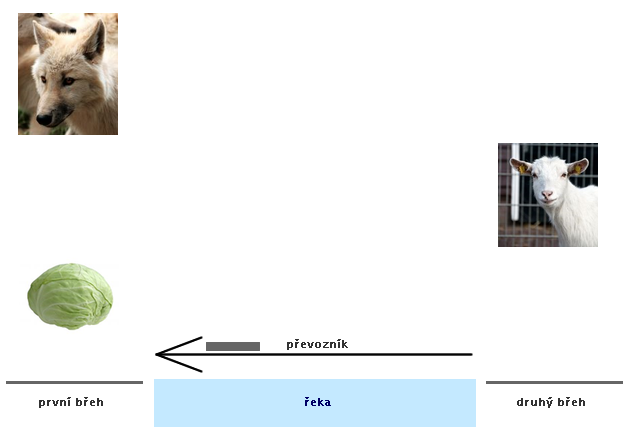
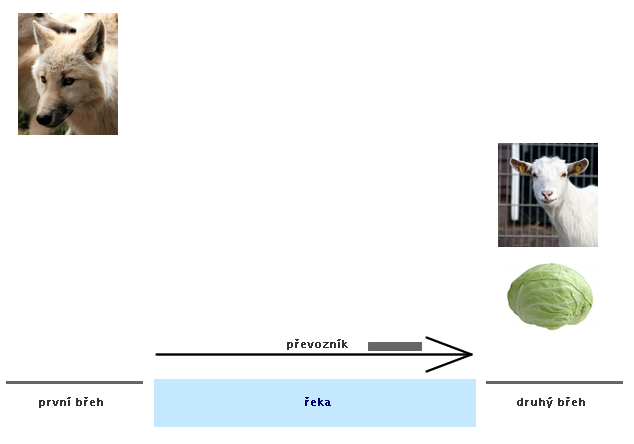
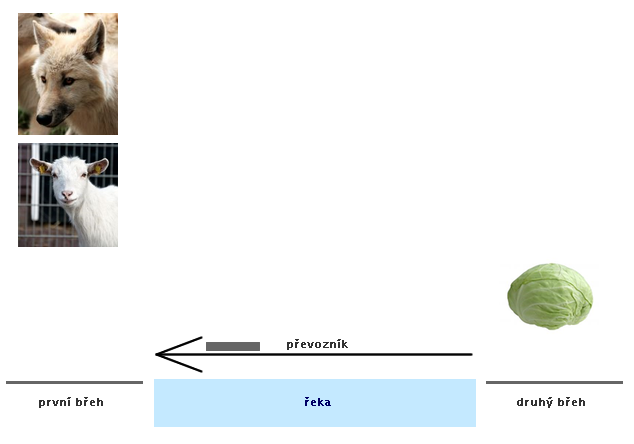

Řešení č. 2 - oranžové hrany (animace)