3. Vybrané problémy / Výroky
Úvod
Výroková logika je další částí matematiky, kde můžeme využít teorii grafů. Možná jste při řešení logických úloh již grafy nebo alespoň podobné zobrazení pomocí bodů a čar použili.
Při řešení těchto úloh budeme používat spojování známých objektů (kterými mohou být osoby, automobily... - jim odpovídají vrcholy grafu) pomocí logických vazeb mezi nimi (ke znázornění logických vazeb typu implikace slouží hrany grafu). Samotný výsledek (pravdivostní hodnoty příslušných výroků) pak zjistíme pomocí barvení uzlů - obdobně jako u barvení mapy.
Princip řešení s použitím základních pravidel si ukážeme na ukázkové úloze.
Zadání [15]
Rekreanti A, B, C, D, E se rozhodují, zda podniknou cestu parníkem. Své rozhodnutí podmiňují někteří tím, jak se rozhodne další z nich. Paní B říká, že pojede, vydá-li se na cestu její manžel A. Pánové A, D rozhodně pojedou, pojede-li šprýmař E. Paní B a slečna C se nemají rády, společně nepojedou "za nic na světě". Slečna C a pan D pojedou jen spolu nebo nepojede žádný z nich. Máme zjistit, kdo nastoupí na parník, je-li jisto, že alespoň jeden z pánů D, E si toto dobrodružství nenechá ujít.
Řešení:
Nejprve si popíšeme vrcholy grafu, se kterými budeme pracovat.
Nemůžeme použít jen pět vrcholů (co osoba, to jeden vrchol), protože některé implikace jsou závislé na tom, že vybraná osoba na výlet nepojede.
Vrcholů bude v grafu celkem 10 - u každé osoby vždy jeden vrchol bude odpovídat situaci, že daná osoba pojede, druhý vrchol, že nepojede.
Pro označení vrcholů použijeme malá písmena - a bude znamenat, že osoba A pojede (a', že osoba A nepojede). Prohlédněte si obrázek č. 3.17.
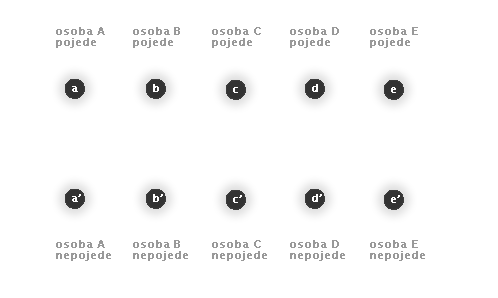
Obr. č. 3.17 - Množina vrcholů pro ukázkovou úlohu
Samotné implikace budeme zakreslovat jako orientované hrany.
Např.: "Paní B říká, že pojede, vydá-li se na cestu její manžel A." zakreslíme jako hranu a→b.
"Paní B a slečna C se nemají rády, společně nepojedou 'za nic na světě'. " - b→c' a c→b' (obr. č. 3.18).
Na této implikaci vidíme, proč jsme museli zavést speciálně i vrcholy pro opačné výroky.
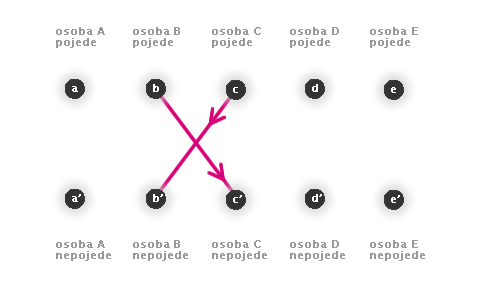
Obr. č. 3.18 - Zakreslení implikace v grafu
Zakreslujeme relaci "z prvního výroku vyplývá druhý" na desetiprvkové množině vrcholů {a, a', b, b', c, c', d, d', e, e'}.
Jak se v našem grafu projeví výroky "alespoň jeden z a a b", "nejvýše jeden z a a b", "právě jeden z a a b", "a právě tehdy, když b"?
Tyto výroky musíme umět převést na jednodušší - pomocí implikací.
"Alespoň jeden z a a b" = znázorníme pomocí šipek a' → b, b' → a
(Pokud není splněno a, musí být splněno b a naopak.)
"Nejvýše jeden z a a b" = vyjádříme pomocí šipek a → b', b → a'
(Pokud je splněno a, nesmí být splněno b a naopak.)
"Právě jeden z a a b" = podobně: a → b', b' → a, a' → b, b → a'
(a je splněno právě tehdy, když není splněno b; a není splněno právě tehdy, když je splněno b)
"a právě tehdy, když b" = buď platí a i b současně, nebo oba výroky současně neplatí (v grafu načrtneme čtyři šipky a → b, b → a, a' → b', b' → a')
Všechny relace z úlohy zakreslené v grafu
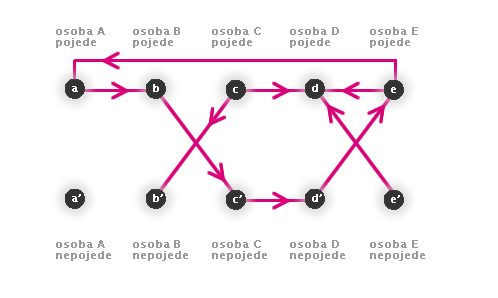
Obr. č. 3.19 - Všechny relace z úlohy zakreslené v grafu
Řešení pomocí barvení vrcholů
Nyní potřebujeme zjistit, jaké je správné řešení úlohy (která osoba pojede a která nikoliv).
Použijeme barvení vrcholů - podobný princip jako u barvení mapy, ovšem jen se dvěma barvami - zelenou, která bude vyjadřovat pravdivý výrok a červenou, , která bude odpovídat nepravdivému výroku.
Pro snazší orientaci v textu bude "zelený vrchol" znamenat vrchol obarvený zeleně (zakresleno zeleným kolečkem) a odpovídající pravdivému výroku, "červený vrchol" bude znamenat vrchol obarvený červeně (červené kolečko, odpovídá nepravdivému výroku).

Obr. č. 3.20 - Příklad zakreslení pravdivého a nepravdivého výroku jako vrcholu v grafu
Na začátku budeme vycházet z libovolného předpokladu o nějakém výroku (například "výrok A platí") a pomocí logických pravidel (následující odstavec) příklad vyřešíme nebo dojdeme ke sporu.
Základní pravidla barvení vrcholů:
- 1: Každý výrok má právě jednu pravdivostní hodnotu.
→ Každý vrchol má právě jednu barvu (je zelený nebo červený). - 2: Výroky x a y mají různou pravdivostní hodnotu.
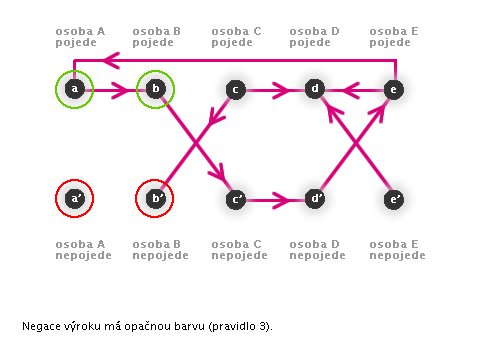
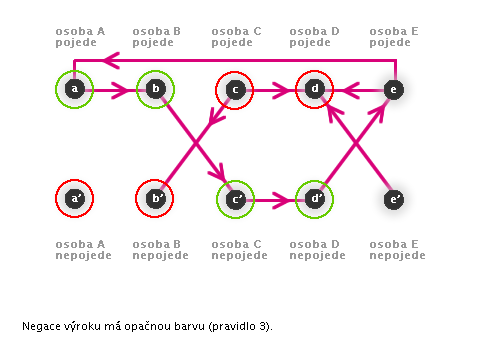
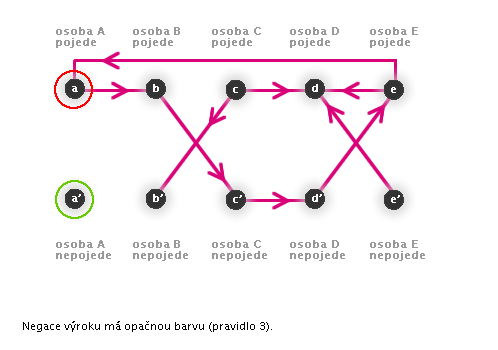
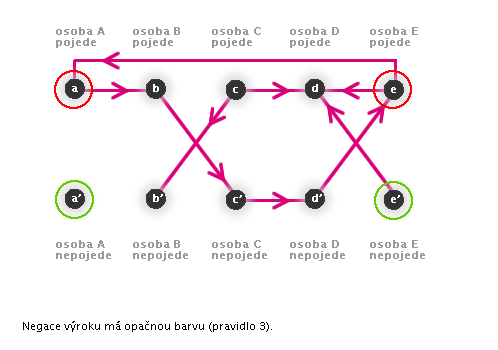
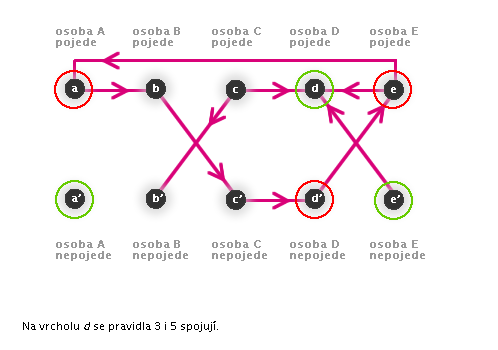
→ Vrcholy x a y mají různou barvu. - 3: Dva vrcholy zakreslené nad sebou mají opačné barvy.
→ Je-li jeden z vrcholů zelený, druhý obarvíme červeně. Je-li červený, druhý obarvíme zeleně.
(Toto pravidlo odpovídá základnímu logickému pravidlu: vždy je pravdivý buď výrok samotný nebo jeho negace.) -
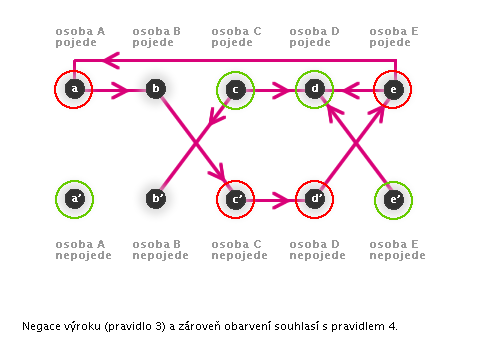
4: Platí-li předpoklad implikace a platí-li implikace, musí platit důsledek.
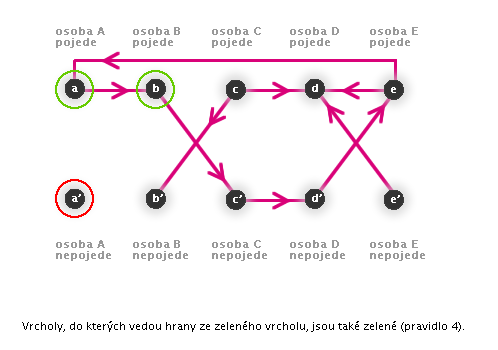
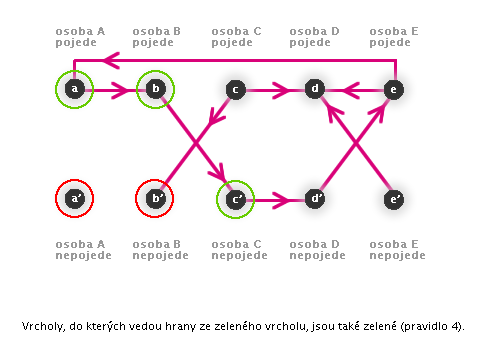
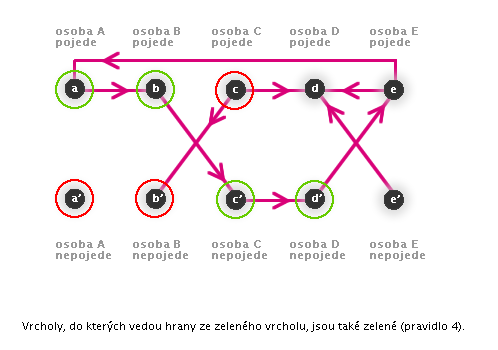
→ Pokud ze zeleného vrcholu směřuje hrana, vrchol, do kterého směřuje, musí být také zelený. -
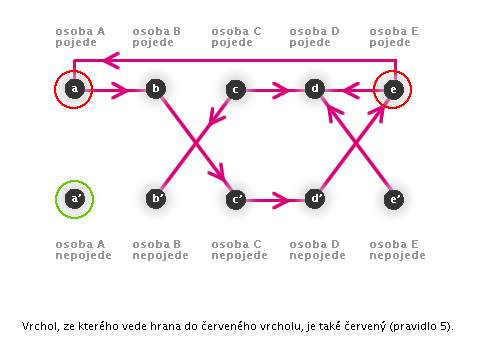
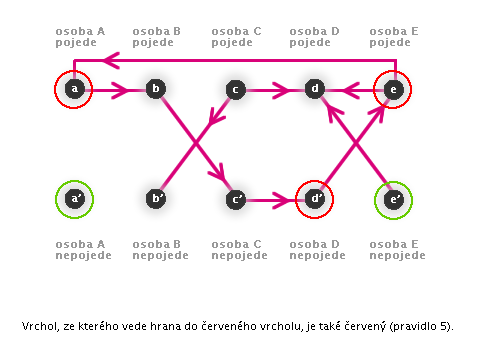
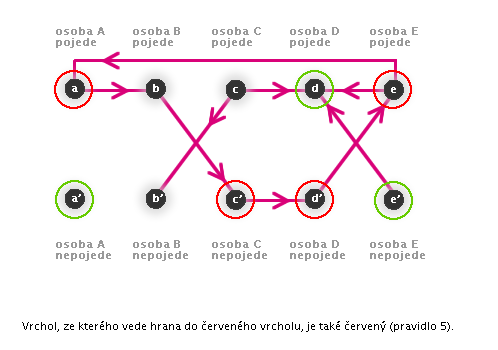
5: Pokud neplatí důsledek implikace a platí-li implikace, neplatí ani předpoklad.
→ Pokud do červeného vrcholu směřuje hrana, vrchol, ze kterého směřuje, musí být také červený.
Příklad, ve kterém při barvení vrcholů dojde ke sporu (animace)
Následující animace znázorňuje možnost, při které dojde k logickému sporu.
V takovém případě dojdeme k závěru, že předpoklad nebyl správný a vyzkoušíme jiný.
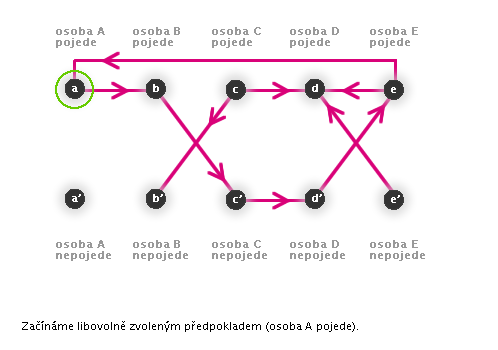
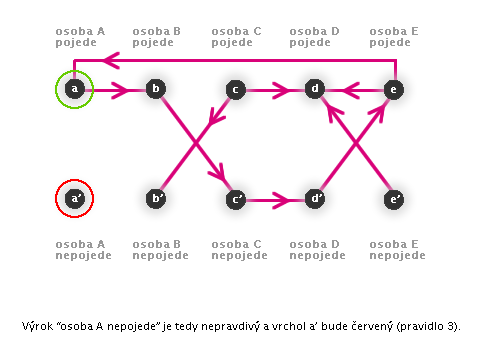
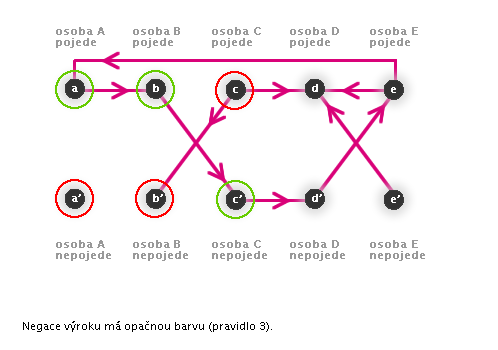
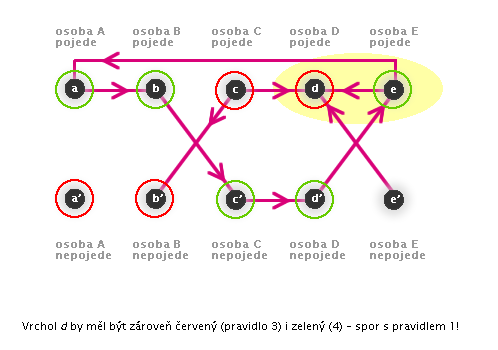

Nyní jsme zjistili, že za předpokladu, že pan A pojede parníkem, není možné splnit všechny požadavky všech cestujících. Nyní mohou nastat 2 situace:
1) předpoklad, že pan A nepojede, rovněž povede ke sporu a ukáže se, že požadavky jednotlivých cestujících jsou navzájem neslučitelné
2) předpoklad, že pan A nepojede, nás dovede k výslednému řešení úlohy.
Příklad, který nalezne hledané řešení (animace)
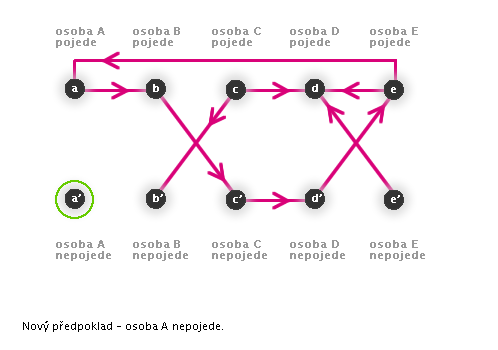
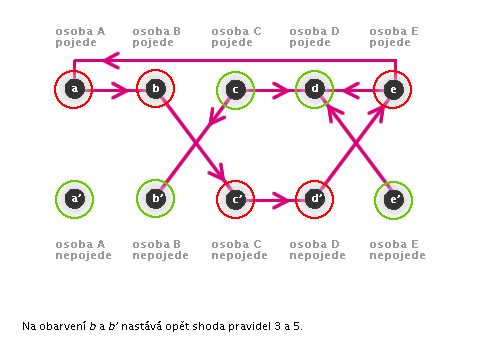
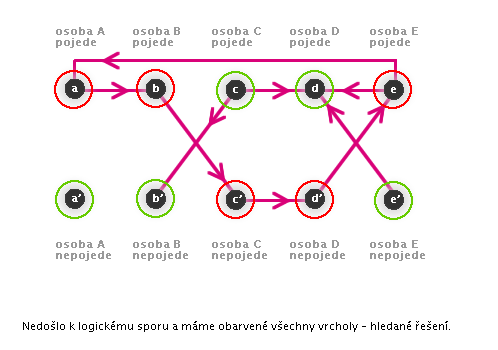

Shrnutí řešení
Hledaným řešením úlohy je situace: na výlet pojede jen osoba C a D.
(Osoby A, B, E nepojedou.)