3. Vybrané problémy / Barvení mapy
Úvod
Pomocí teorie grafů lze dokázat, že pro obarvení libovolné mapy tak, aby dvě sousední země nebyly obarveny stejnou barvou, nám postačí čtyři barvy.
Příklad mapy obarvené čtyřmi barvami
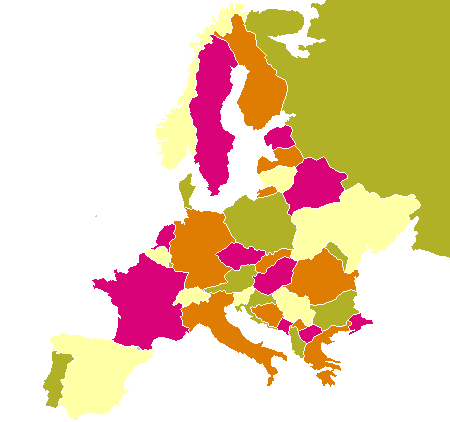
Obr. č. 3.7 - Politická mapa obarvená čtyřmi barvami (viz [7])
Spojitost s teorií grafů
Pro řešení tohoto problému použijeme podobný princip jako u Eulerovy úlohy - každý stát si představíme jako vrchol grafu a hranou spojíme státy, které spolu sousedí. Místo obarvení si také můžeme představit dosazování čísel k vrcholům. Díky tomu lze také formulovat problém matematicky (následuje).
Poznámka: Barvení grafu se řeší pro souvislé grafy, proto jsme z mapy vymazali ostrovy (např. Velkou Británii).
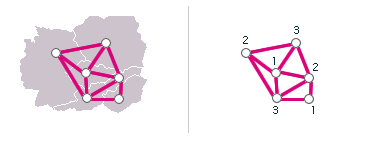
Obr. č. 3.8 - Spojitost mezi barvením mapy a grafem, který této mapě odpovídá
Zadání matematicky
Nechť G = (V,E) je graf, k přirozené číslo. Zobrazení b: V → {1,2,...,k} nazveme obarvením grafu G pomocí k barev, pokud pro každou hranu {x,y} 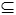 E platí b(x)
E platí b(x) 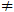 b(y).
b(y).
Poznámka
Někdy může nastat situace, že státy sousedí jedním bodem. V takovém případě není nutné, aby měly všechny státy různé barvy.

Obr. č. 3.9 - Státy sousedící jedním bodem
Proč čtyři barvy?
Nejprve se podívejme, proč potřebujeme nejméně 4 barvy:
- Mějme 1 barvu: Úlohu bychom nemohli vyřešit. Mají-li mít sousední státy rozdílné barvy, nemohli bychom obarvit ani dva sousedy (např. ČR a SR).
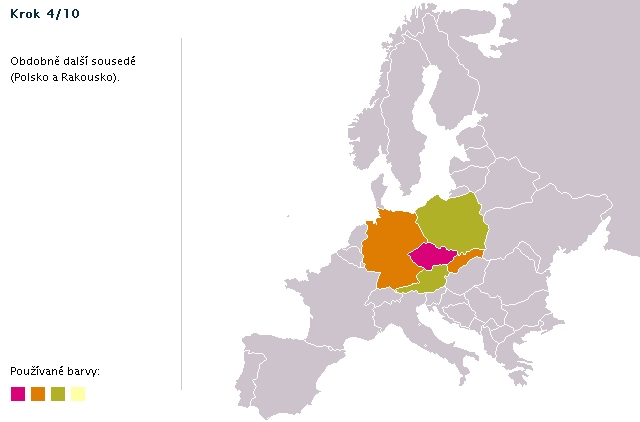
- Mějme 2 barvy: Podobná situace - dejme ČR první barvu, SR i Něměcku druhou. Polsko ovšem sousedí i s ČR (barva 1), SR (barva 2) i Něměckem (barva 2). Proto potřebujeme třetí barvu.
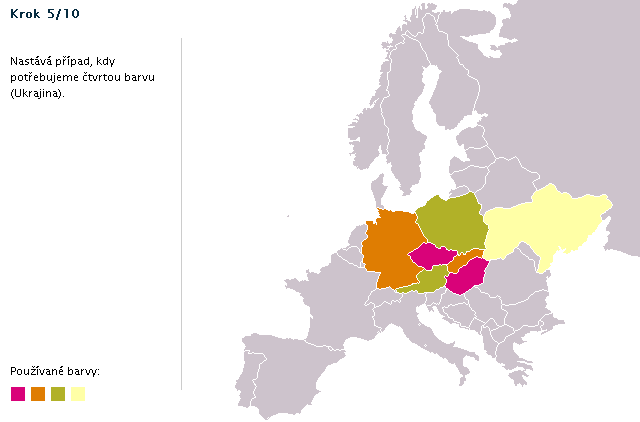
- Mějme 3 barvy: Na obrázku č. 3.10 vidíme, že pro Ukrajinu (označena otazníkem) se nám opět nedostává barev - máme již obarvené tři sousedy (každý má jinou barvu) - znovu potřebujeme další barvu.
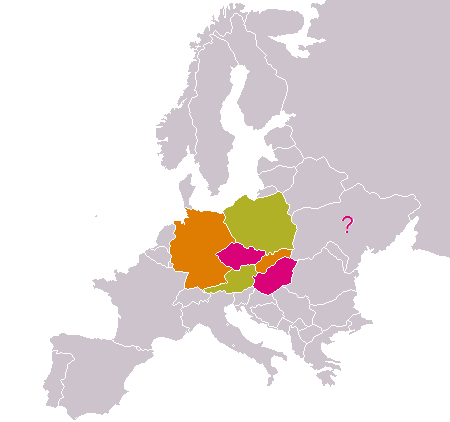
Obr. č. 3.10 - Proč potřebujeme při barvení mapy čtyři barvy?
Proč nám čtyři barvy už stačí? - viz rámeček Důkaz....
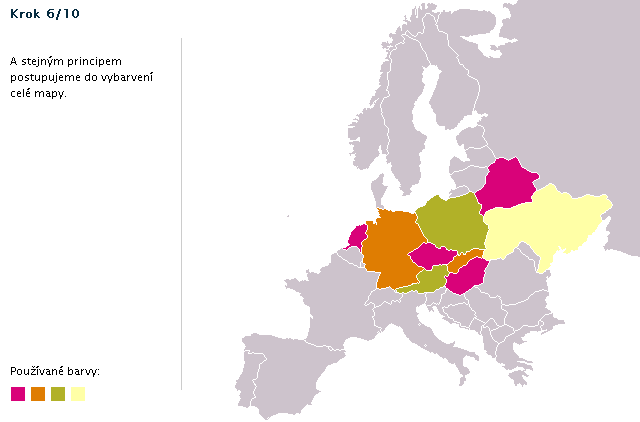
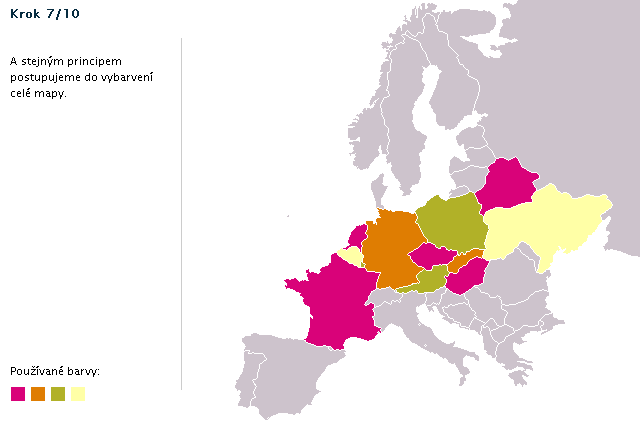
Postup obarvení ukázkové mapy (animace)
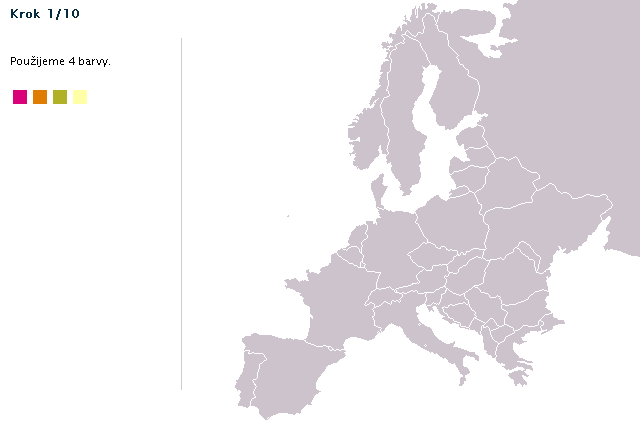
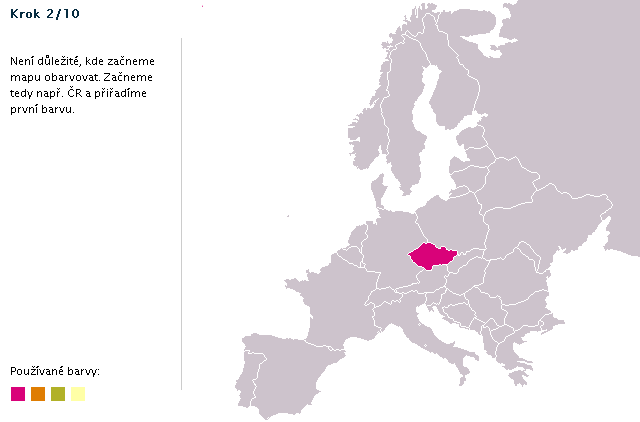
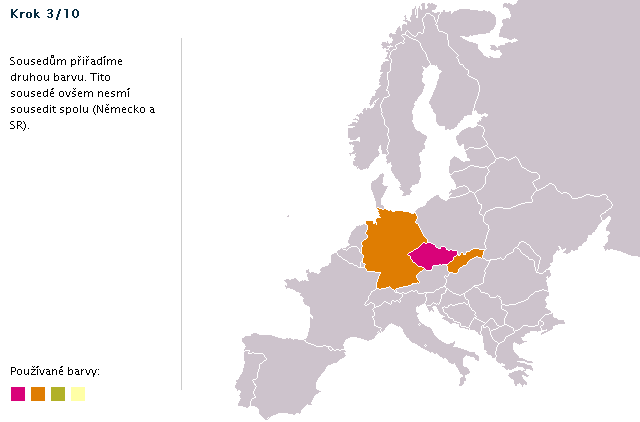
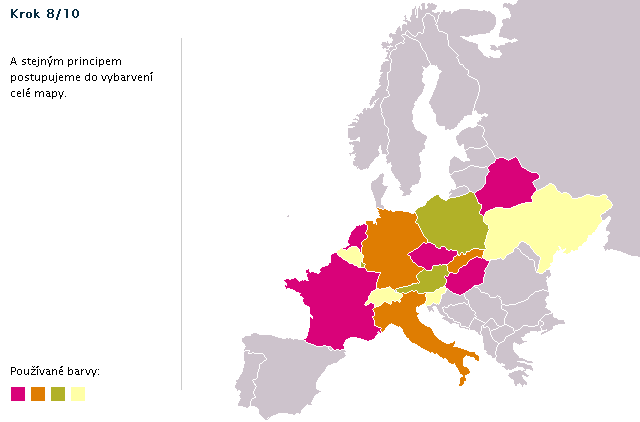
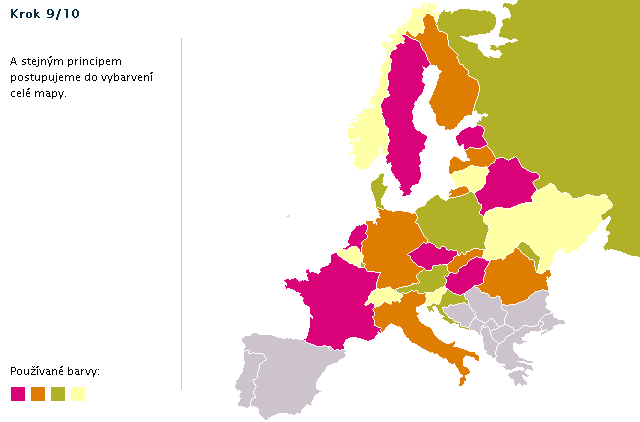
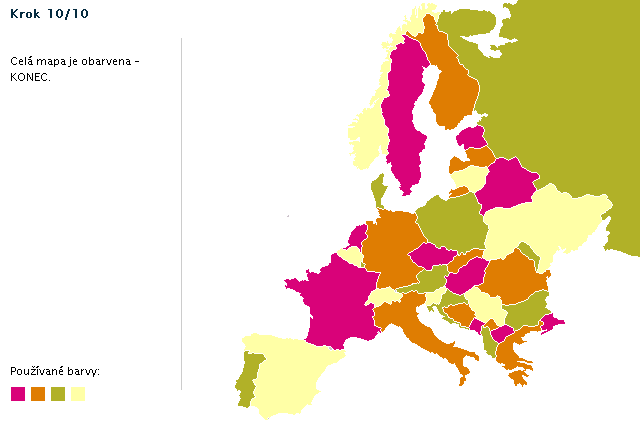

Důkaz, že pro obavení mapy stačí čtyři barvy
Dokázat, že pro obarvení libovolné mapy stačí čtyři barvy, je matematicky poměrně náročný. Problém byl vyřešen v 70. letech 20. století, přičemž velká část problému byla dokázána pomocí počítače - viz [12] a [13].
Důkaz jednoduššího tvrzení (pro obarvení stačí 5 barev) můžete najít v knize [1], str. 214.
Praktické využití
Podobný problém (na složitější úrovni) se řeší v mobilních sítích. Oblast je rozdělena na mnoho malých buňek, ve kterých telefony komunikují se základnovými stanicemi na určité frekvenci. Snahou operátorů je využít co nejmenší počet frekvencí (odpovídající co nejmenšímu počtu barev) a přitom respektovat nutnou podmínku, že sousední buňky nemohou být nastaveny na stejnou frekvenci (což by odpovídalo obarvení sousedních států stejnou barvou).