3. Vybrané problémy / Hledání minimální kostry v grafu
Úvod
Úloha hledání minimální kostry nám popisuje, jak máme spojit všechny vrcholy grafu "co nejlevněji" - hranami s nejnižší váhou (ohodnocením). Praktickým využitím mohou být například rozvody elektřiny mezi městy - jak propojit města co nejmenší délkou elektrického vedení.
Definice minimální kostry
Hledání minimální kostry má smysl u ohodnocených grafů. Podobně jako u vzdáleností si zavedeme funkci w, která hranám přiřadí číslo - tzv. váhu.
Zadání problému pak můžeme matematicky zapsat takto:
Pro souvislý graf G = (V,E) s nezáporným ohodnocením hran w najděte souvislý podgraf (V,E') takový, že výraz:
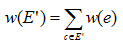
nabývá minimální hodnoty.
Kruskalův algoritmus
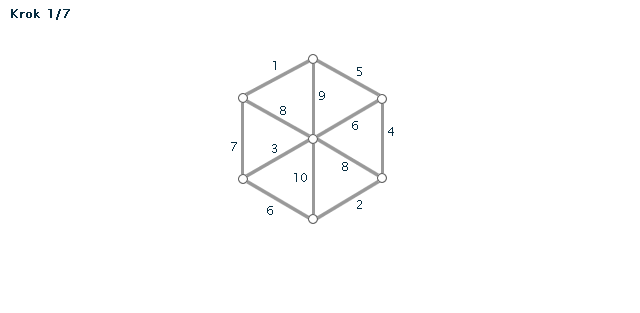
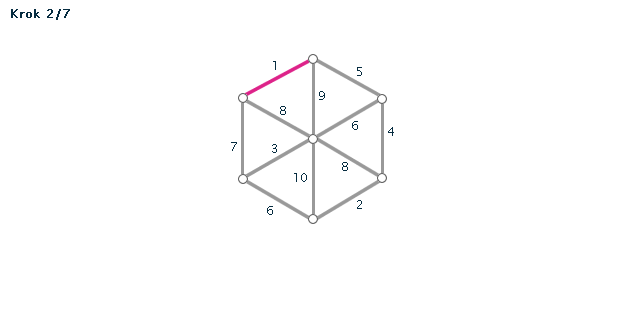
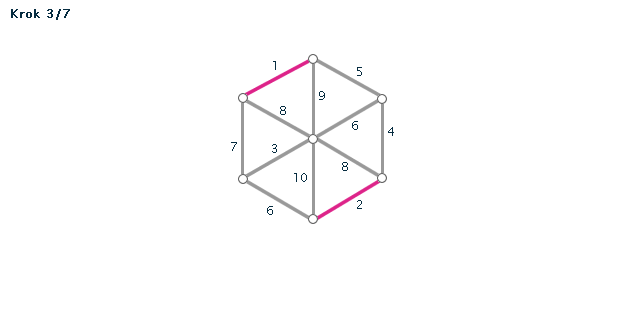
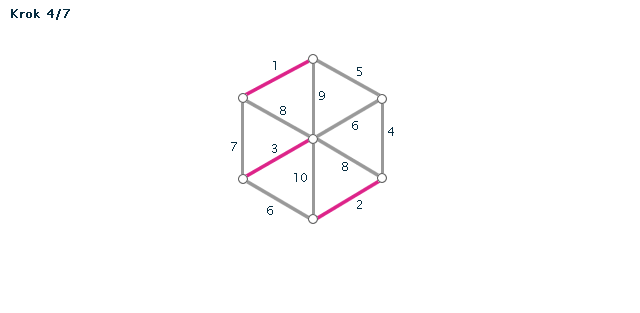
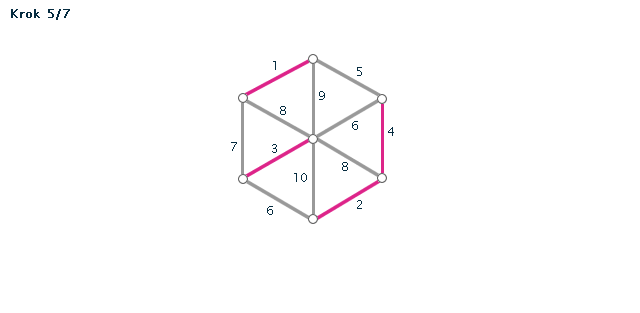
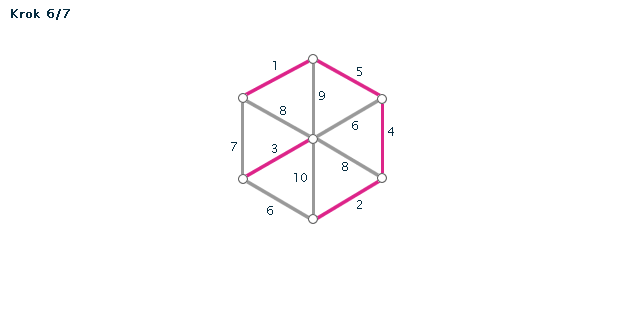
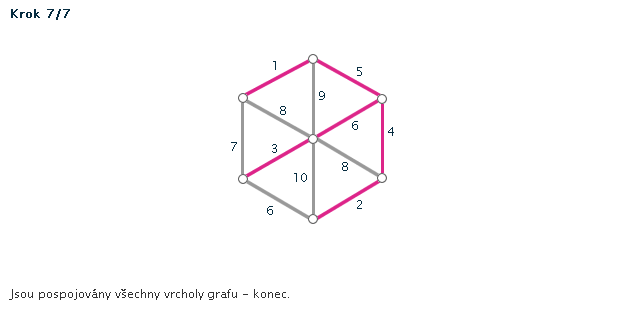
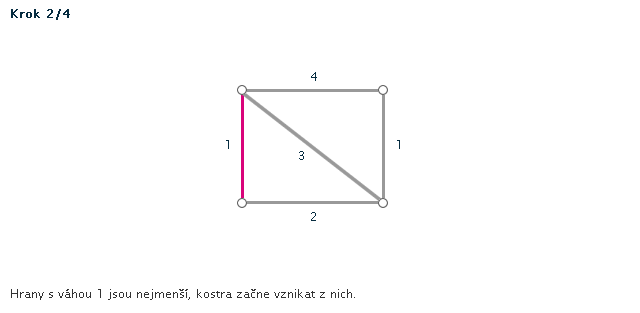
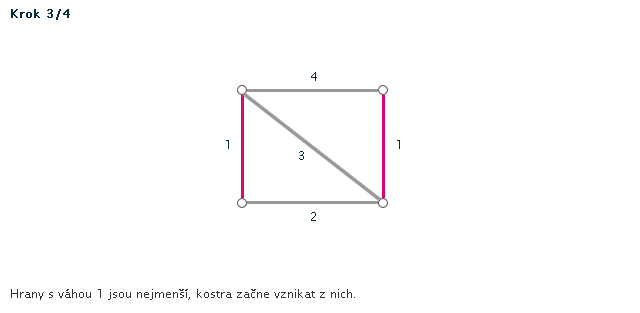
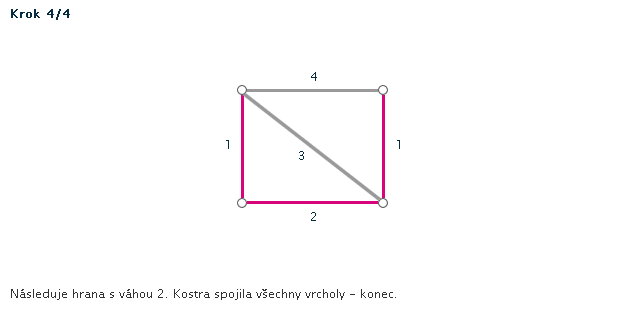
Kruskalův algoritmus je jedním z algoritmů pro hledání minimální kostry grafu. Pracuje na principu spojování hran s nejmenším ohodnocením, dokud tyto hrany nespojí vrcholy celého grafu. Díky jeho snadnému postupu jej lze snadno použít i bez počítače při "ručním výpočtu" - v procvičování si můžete zkusit některé úlohy vyřešit sami za použití zvýrazňovače.
Popis Kruskalova algoritmu
- Všechny hrany si seřadíme podle velikosti (vzestupně - od hrany s nejmenší váhou).
- Hranu s nejmenší váhou použijeme jako první hranu kostry.
- Pokud jsme tím už vytvořili kostru (graf měl jen dva vrcholy), končíme. V opačném případě vezmeme hranu s druhou nejmenší váhou.
POZOR! Pokud by nám v grafu vznikla kružnice, hranu nepoužijeme. - Opakujeme minulý krok, dokud vznikající kostra nespojí všechny vrcholy grafu.
Kruskalův algoritmus matematicky
Je dán souvislý graf G = (V,E) s n vrcholy, m hranami a s ohodnocením w. Očíslujme hrany e1, e2,...,em tak, aby:
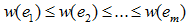 .
.
Nyní budeme postupně konstruovat množiny hran E0, E1, E2,... 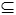 E.
E.
Položme E0 = 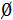 .
.
Byla-li již nalezena množina Ei-1, určíme množinu Ei následovně:

Algoritmus se zastaví, jestliže buď Ei již obsahuje n-1 hran, nebo i = m, tj. probraly se všechny hrany grafu G. Nechť Et značí množnu, pro níž se algoritmus zastavil, a nechť T značí graf (V,Et). T je pak hledanou minimální kostrou.
Kruskalův algoritmus je tzv. hladový.
Co jsou hladové algoritmy?
Za hladové algoritmy jsou označované takové algoritmy, které vždy volí v danou chvíli nejvýhodnější volbu (aniž by se snažily "myslet do budoucnosti").
Anglicky jsou označovány greedy search (greedy = chamtivý).
Příklad špatného užití podobného principu by bylo např. při hraní šachů - podobným postupem by hráč téměř jistě prohrál. Naopak u některých úloh (zmiňované hledání minimální kostry) funguje takový algoritmus úspěšně.
Příklad č. 1 (animace)
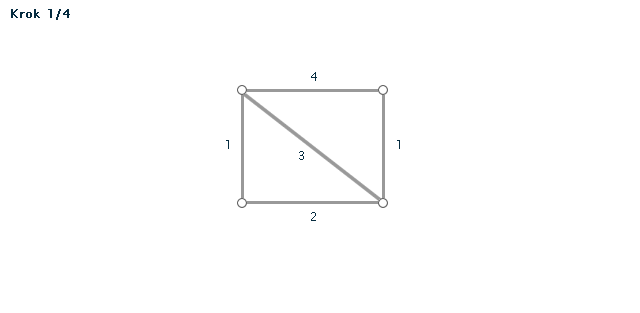

Příklad č. 2 (animace)
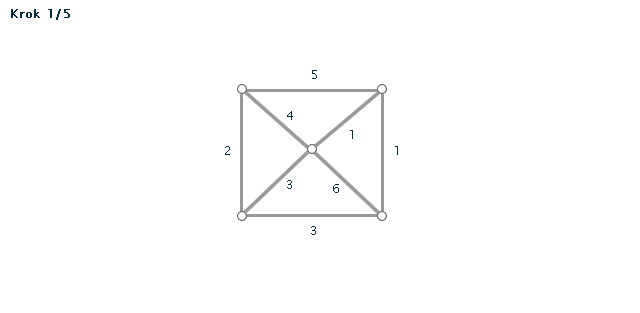
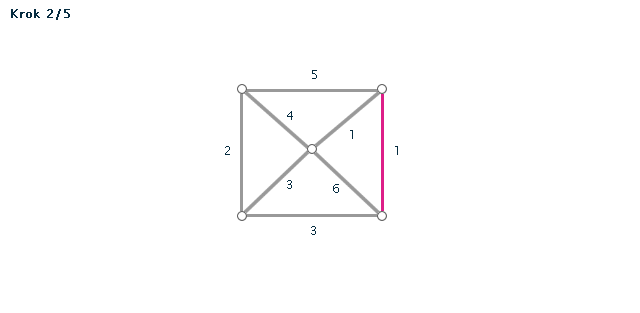
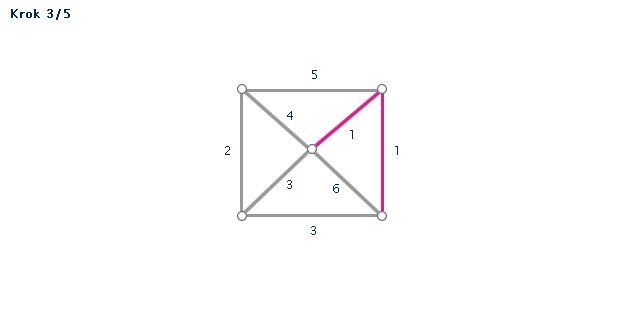
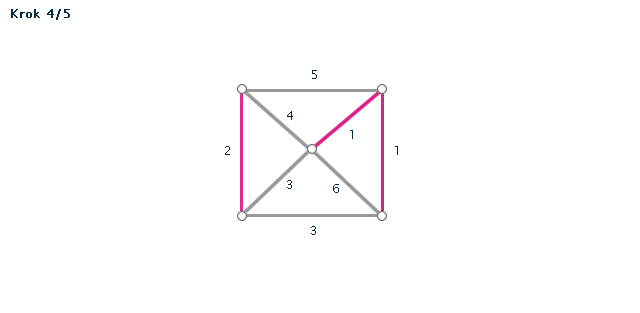
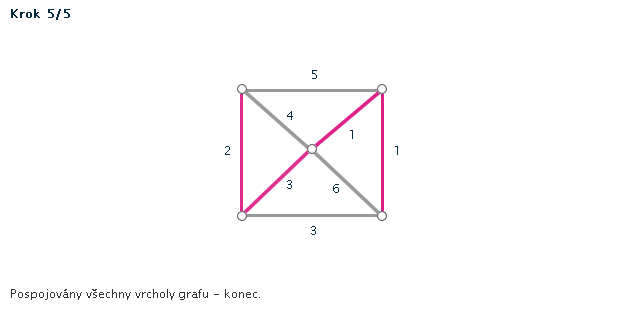

Příklad č. 3 (animace)
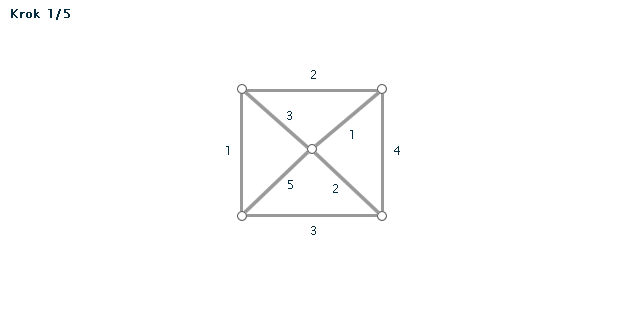
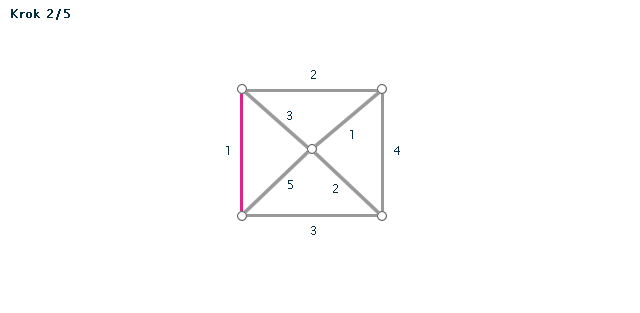
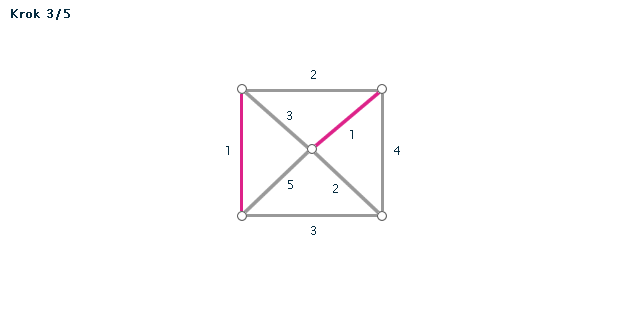
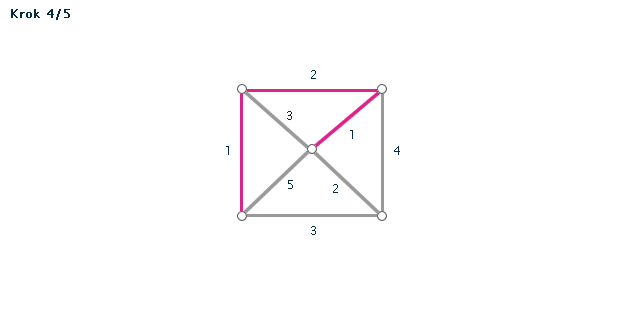

Příklad č. 4 (animace)