4. Procvičování / Otáčení skleniček
Úloha [18]
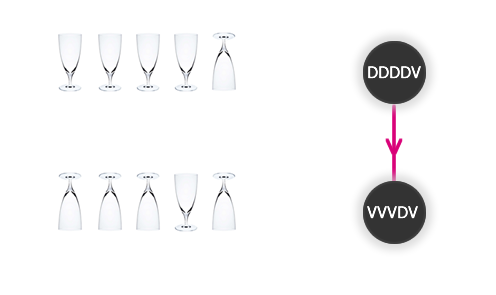
Na stole stojí v řadě pět skleniček vedle sebe. Čtyři z nich (nevíme, které) jsou dnem vzhůru a jedna dnem dolů. Úkolem je otočit všechny skleničky dnem dolů. V jednom tahu můžete otočit vždy pouze tři sousední skleničky.
Nalezněte počáteční rozmístění skleniček, pro které je úloha řešitelná.
Nápověda
Rozkreslete si možnosti pomocí grafu, ve kterém bude každému vrcholu odpovídat jedno rozestavení skleniček (např. VDVVV - skleničky v řadě dnem vzhůru, dolů, vzhůru, vzhůru, vzhůru) a každé hraně přípustné otočení skleniček.
Řešení
Úlohu začneme řešit od konce.
Známe koncový stav, do kterého se chceme dostat (všechny skleničky jsou otočené dnem dolů - DDDDD).
Víme také, že pro každé uspořádání skleniček máme jen tři možnosti změny - otočíme první, druhou a třetí; druhou, třetí a čtvrtou či třetí, čtvrtou a pátou.
Do každého vrcholu proto povedou tři hrany - budeme kreslit vrcholy (od stavu DDDDD do stavů, ze kterých stav nastal otočením tří skleniček, dokud nenalezneme vrchol, který by odpovídal zadání (čtyři skleničky dnem vzhůru a jedna dnem dolů).
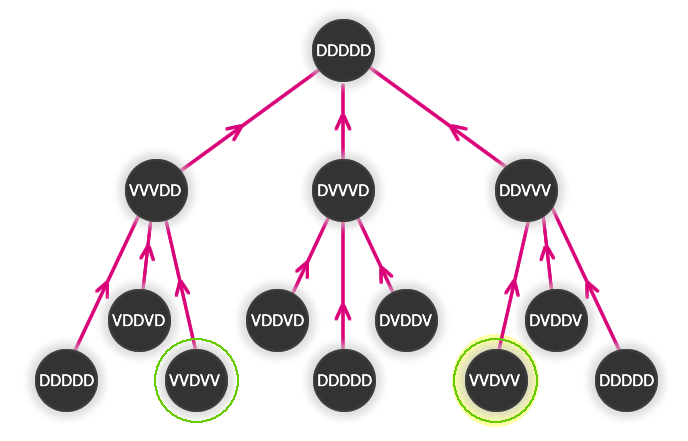
Takové vrcholy najdeme dva - oba přitom odpovídají stavu, kdy je směrem dolů otočená prostřední sklenička - VVDVV.
To je hledané řešení naší úlohy.