3. Vybrané problémy / Jednotažky (eulerovské grafy)
Úvod
Kreslení grafů jedním tahem je jednou ze základních úloh teorie grafů - viz Eulerova úloha o procházení po mostech. Pro zjednodušení si úlohu předvedeme na neorientovaných grafech, podobný problém lze řešit i na orientovaných grafech.
Zadání
Nakreslete daný graf G = (V,E) jedním uzavřeným tahem bez zvednutí tužky papíru (žádna hrana se neobtahuje dvakrát). Tento tah začíná i končí ve stejném vrcholu.
Příklad (animace)
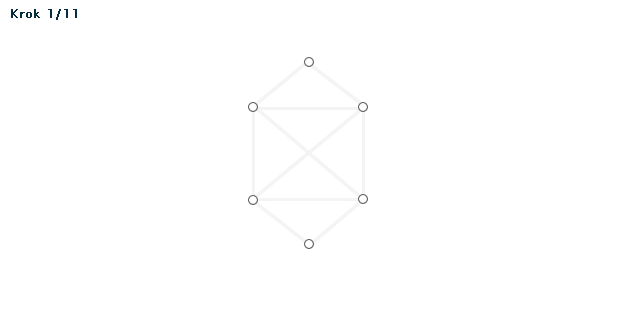
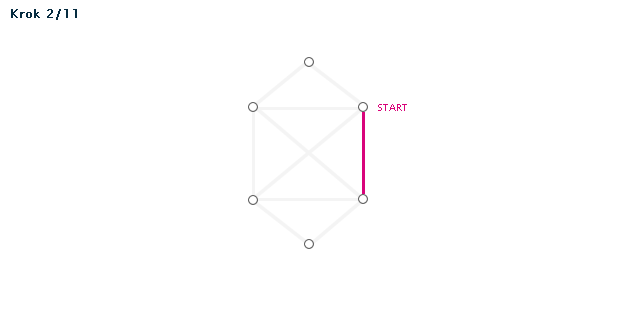
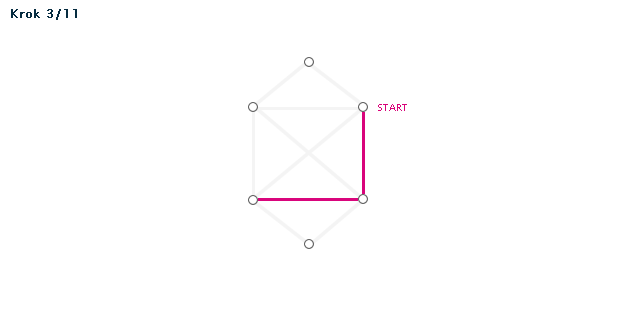
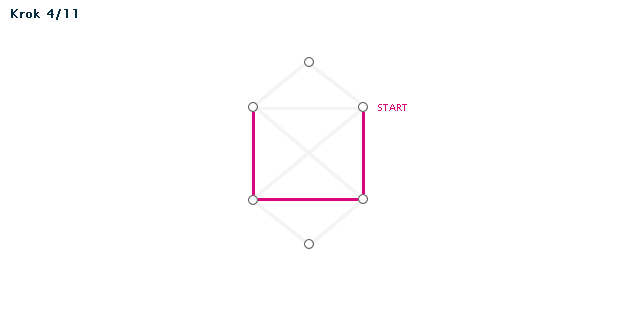
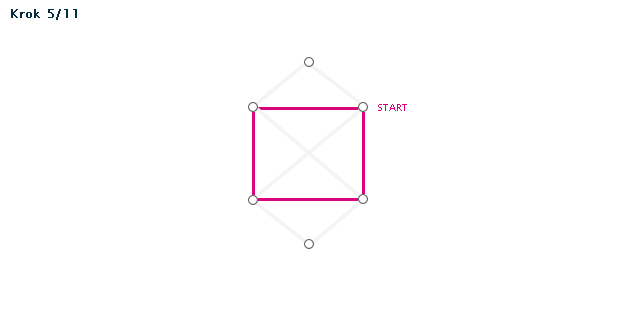
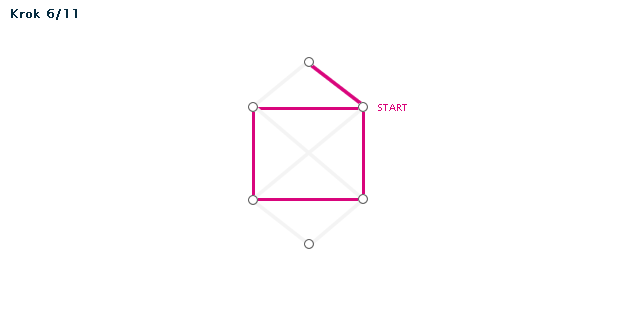

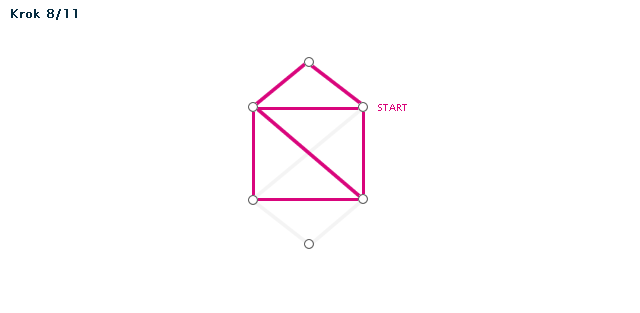
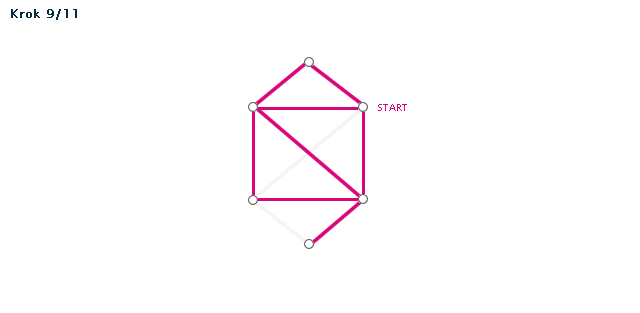
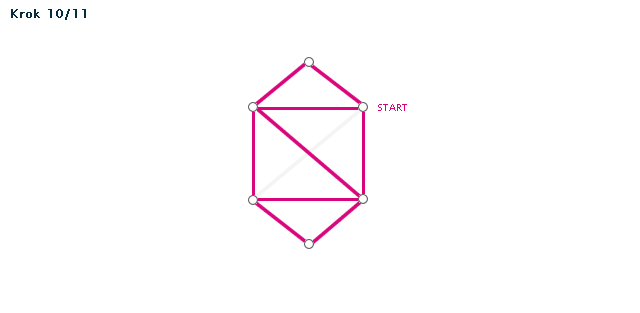
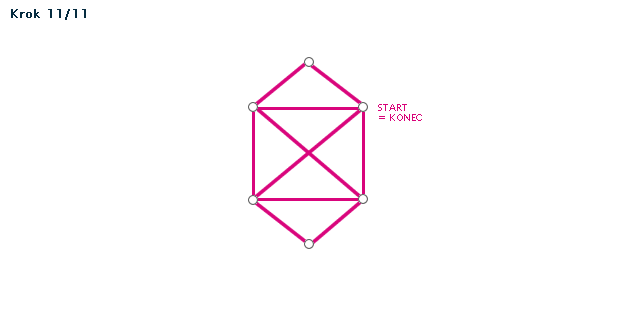

Poznámka
Nalezený tah není jediný možný. Tah může začínat (resp. končit) v libovolném vrcholu.
Návod
Graf G je eulerovský, právě když je souvislý a každý vrchol G má sudý stupeň.
Eulerova úloha Sedm mostů Königsbergu
Předchozí věta také vysvětluje, proč je úloha Sedmi mostů města Königsbergu (viz historie) neřešitelná - ačkoliv je graf souvislý, neplatí, že by všechny vrcholy měly sudý stupeň (naopak všechny mají lichý stupeň).
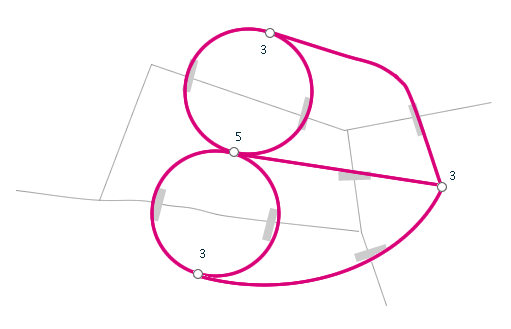
Obr. č. 3.5 - Proč nelze vyřešit úloha Sedmi mostů města Königsbergu?
Otevřené tahy
V literatuře také můžeme najít termín otevřený eulerovský tah - je definován stejně jako tah uzavřený, pouze se nevrací do původního bodu, kde začal.
Jsou-li v grafu právě dva vrcholy lichého stupně, pak existuje otevřený eulerovský tah začínající v jednom z těchto vrcholů a končící v druhém. [5]
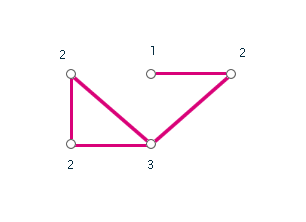
Obr. č. 3.6 - Otevřený eulerovský tah