3. Vybrané problémy / Počty koster grafu
Pro počet koster grafu neplatí žádné jednoduché univerzální pravidlo - většinou si musíme všechny možnosti představit podobně jako obdobné příklady v kombinatorice.
Platí však několik speciálních pravidel podle toho, o jaký graf se jedná:
Počty koster úplného grafu (Cayleyho formule)
Pomocí Cayleyho formule můžeme určit počet stromů na daných n vrcholech - tedy počet koster úplného grafu.
Pro každé n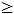 
3 je počet stromů na daných n vrcholech roven nn-2.
Počty koster kružnice
Pokud je graf kružnicí, je počet koster grafu roven |V| (|V| = |E|, můžeme vynechat vždy právě jednu hranu).
Obr. č. 3.1 - Příklad různých koster kružnice
Počty koster stromu
Pokud je graf stromem, má právě jednu kostru (samotný graf je kostrou).
Příklad
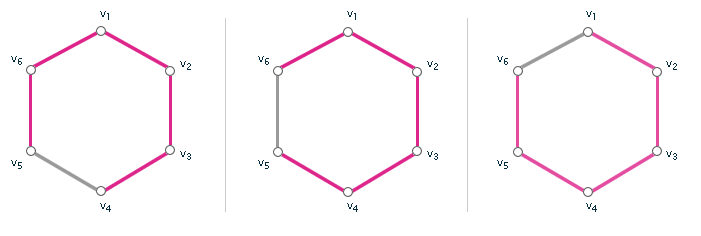
Budeme-li chtít zjistit, kolik různých koster má následující graf (obr. č. 3.2), můžeme si jej rozdělit na jednotlivé podgrafy a výsledek pak získáme vynásobením počtů koster jednotlivých podgrafů (kombinatorické pravidlo součinu).
Obr. č. 3.2 - Příklad výpočtu počtu koster pomocí podgrafů
Na obr. č. 3.2 máme u prvního podgrafu (podgrafy jsou odděleny přerušovanými čarami) 3 možnosti, jak zvolit kostru (jde o kružnici). V druhém podgrafu je pouze jedna možnost výběru hrany (pokud bychom tuto jedinou hranu nevybrali, graf by přestal být souvislým a tím by porušil definici kostry). V třetím podgrafu máme opět 3 možnosti výběru.
Výsledkem je tedy součin 3×1×3 = 9 - máme tedy 9 různých koster grafu.
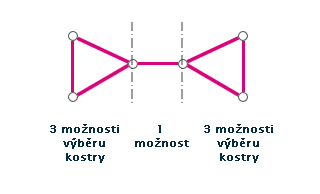
Obr. č. 3.3 - Všechny různé kostry daného grafu