2. Základní pojmy / Cesta a souvislost v grafu
Cesta
Definice
Cestu v grafu můžeme chápat jako posloupnost vrcholů a hran (v0, e1, v1,..., et, vt), kde vrcholy v0,..., vt jsou navzájem různé vrcholy grafu G a pro každé i = 1,2,...,t je ei = {vi-1, vi} 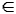 E(G).
E(G).
Poznámka: Tato definice povoluje i cestu délky 0.
Příklad cesty v grafu
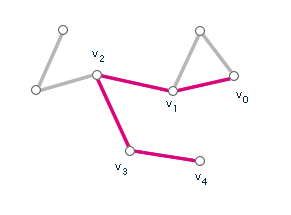
Obr. č. 2.10 - Příklad cesty v grafu (v0, v1, v2, v3, v4)
Souvislost
Někdy potřebujeme vyjádřit, jestli je graf "jedním celkem" - můžeme-li se dostat z každého vrcholu nějakou cestou do jiného, nebo zda jde o více na sebe nenavazujících částí.
Proto se zavádí pojem souvislost grafu:
Definice
Řekneme, že graf G je souvislý, jestliže pro každé jeho dva vrcholy x a y existuje v G cesta z x do y.
Příklad souvislého a nesouvislého grafu
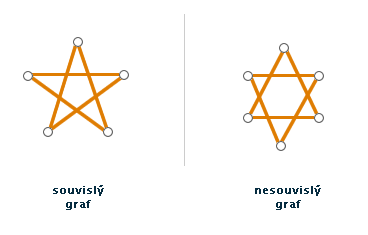
Obr. č. 2.11 - Souvislý a nesouvislý graf
Pokud graf není souvislý, části, ze kterých se skládá (a které jsou samy o sobě souvislé), se nazývají komponenty souvislosti. Na obr. č. 2.11 vpravo by byly komponentami dva trojúhelníky.