4. Procvičování / Úloha s kamarády
Úloha z matematické olympiády [3]
Ve skupině šesti lidí existuje právě 11 dvojic známých. Vztah "znát se" je vzájemný, tzn. jestliže osoba A zná osobu B, pak B zná A. Pokud se kdokoliv ze skupiny dozví nějakou zprávu, řekne ji všem svým známým. Dokažte, že se tímto způsobem zprávu dozví nakonec všichni.
Nápověda
Kamarády si zakreslete jako vrcholy, vztah "znát se" použijte pro hrany a využijte vlastnosti úplných grafů.
Řešení
Kamarády (známé) si zakreslíme jako graf o šesti vrcholech. Graf bude neorientovaný.
Představme si situaci, že se zná každý s každým - půjde o úplný graf o 15 vrcholech (stačí dosadit do vzorce pro výpočet počtu hran v úplném grafu).
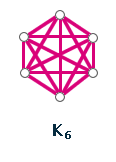
K6 - úplný graf na šesti vrcholech
Ze zadání víme, že hran v grafu bude 11, tzn. z grafu 4 hrany odebereme. Každý vrchol je ale spojen s ostatními 5 vrcholy, takže i pokud odebereme 4 hrany jednomu vrcholu, graf stále zůstane souvislý (→ každá zpráva se dostane ke všem kamrádům).