Teorie grafů

2. Základní pojmy / Kružnice (cyklus) v grafu

Definice

Kružnicí (cyklem) v grafu rozumíme posloupnost vrcholů a hran (v₀, e₁, v₁,..., e_t, v_t = v₀), kde vrcholy v₀,..., v_t-1 jsou navzájem různé vrcholy grafu G a pro každé i = 1,2,...,t je e_i = {v_i-1, v_i} 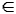E(G).

Poznámka

Nejkratší kružnicí je trojúhelník (K₃ - úplný graf se třemi vrcholy).

Povšimněte si, že definice kružnice se podobá definici cesty - opět jde o posloupnost hran a vrcholů. Na rozdíl od cesty je ale první a poslední vrchol posloupnosti stejný. V cestě ale povolujeme i délku 0 (prázdnou posloupnost). Kružnice má přitom minimální délku 3.

Příklady

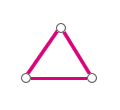
Obr. č. 2.12 - Nejkratší kružnice (trojúhelník)

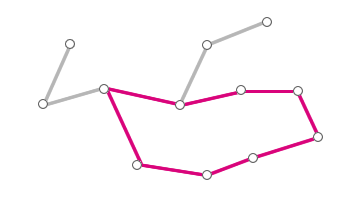
Obr. č. 2.13 - Kružnice v obecném grafu

Acyklický graf

Graf nazýváme acyklický, pokud neobsahuje cyklus.