2. Základní pojmy / Jádro grafu
Jádro grafu je speciální podgraf splňující určité podmínky (viz následující definice), který hledáme u orientovaných grafů. Využívá se často v teorii her.
Definice
Nechť G = (V,E) je orientovaný graf. Množinou W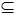 
V (tedy podmnožinu množiny vrcholů) nazveme jádrem grafu G, jestliže platí následující dvě podmínky:
1. Je-li (u0, u1)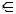 
E a u0 
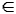W, pak u1 
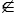W.
2. Jestliže u0 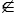W, pak existuje u1 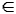W tak, že (u0, u1) 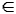E.
Je jádro grafu souvislým grafem podle definice (podobně jako kostra grafu)?
Není. Podle definice jádro neobsahuje žádné hrany, graf tedy nemůže být souvislý.
Pokuste se podmínky 1. a 2. z definice popsat slovy bez použití matematické symboliky
1. Máme-li hranu vycházející z vrcholu, který je v jádru grafu, pak vrchol, do kterého daná hrana směřuje, v jádru grafu není.
2. Pokud nějaký vrchol u0 v jádru není, potom existuje vrchol, který v jádru je, a do kterého vede hrana z u (z každého vrcholu, který není v jádru, vede hrana do nějakého vrcholu v jádru).
Příklady
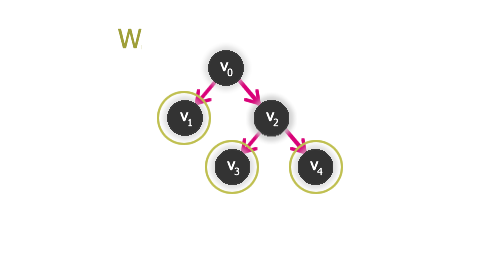
Obr. č. 2.31 - Příklad jádra grafu (množina W skládající se z bodů v1, v3, v4)
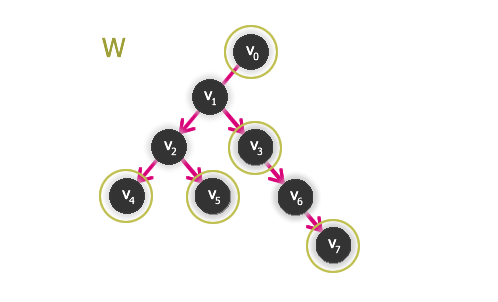
Obr. č. 2.32 - Příklad jádra grafu (množina W skládající se z bodů v0, v3, v4, v5, v7)
Poznámky
Pro každý orientovaný acyklický graf existuje jednoznačně určené jádro.
Důkaz této věty slouží také jako návod, jak jádro najít - viz konstrukce.
Konstrukce
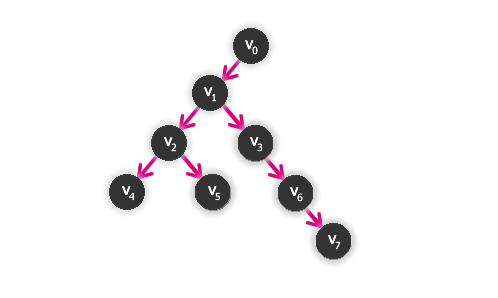
Mějme následující orientovaný graf G, ke kterému hledáme jádro.
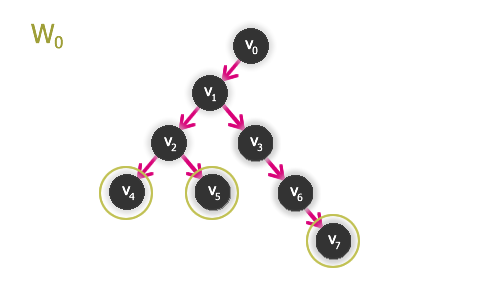
1. Označíme jako W0 množinu vrcholů, které nejsou počátečním vrcholem žádné hrany. W0 bude počátek hledaného jádra.
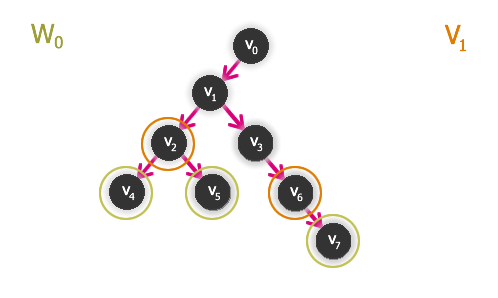
2. Množinu vrcholů, ze kterých směřují hrany do vrcholů ve W0, označíme V1. Pozor: množina V1 není součástí jádra.
3. Nyní si zkontrolujeme, zda "nám nezbyly nějaké vrcholy" - tedy zda graf G \ (V1 
W0) je prázdná množina. Pokud ano, našli jsme jádro původního grafu.
Vidíme však, že nám ještě zbývají vrcholy v0, v1, v3.
Tyto zbývající vrcholy (i s hranami) si označíme jako graf G', indukovaný podgraf grafu G.
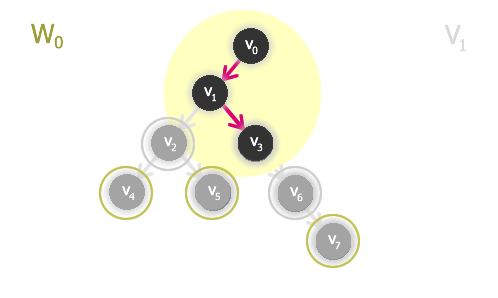
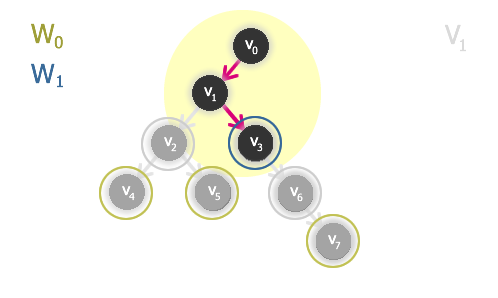
4. Stejně vyřešíme problém pro graf G' a výsledek (jádro G') připojíme k W0. Hledaným výsledkem - jádrem grafu G bude množina vrcholů množiny W0 doplněná o jádro G'.
Pokud ani tak nenalezneme řešení (opět nám "zbudou" vrcholy), pokračujeme stále rekurzivně až do vyřešení celé úlohy (vytvoříme indukovaný podgraf, nalezneme jeho jádro a jeho vrcholy připojíme k předchozímu jádru).
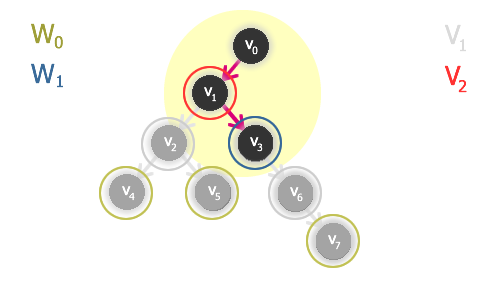
V našem konkrétním příkladě tato situace nastane u vrcholu v0. Ten je sám o sobě podgrafem G'', je jediný koncový vrchol, jádrem grafu G'' je tedy vrchol v0 (resp. množina W2 obsahující pouze v0).
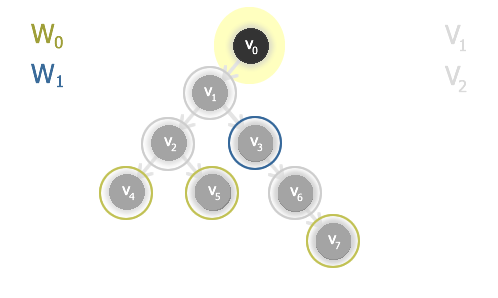
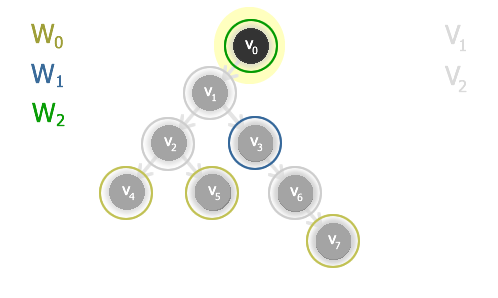
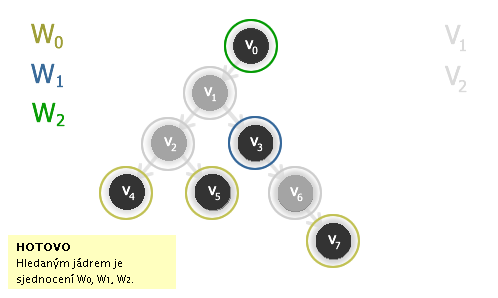
Vrchol v0 přidáme k výsledku pro graf G' (bez grafu G'') - vrcholu v3 a tyto dva vrcholy připojíme k nalezenému jádru G bez G' - vrcholům v4, v5 a v7.
Výsledek: jádrem grafu G je sjednocení množin W0, W1 a W2, tedy množina vrcholů {v0, v3, v4, v5, v7}.
Zobrazení všech kroků jako animace