3. Vybrané problémy / Rozvrh
Úvod
Podobný princip, jaký jsme využili v úlohách s barvením mapy a o výrocích, lze úspěšně použít i při hledání optimálního rozvrhu.
Zadání [16]
Mějme 6 hodin (lekcí) označených h1 až h6, mezi kterými si mohou studenti vybírat. Všechny lekce trvají stejně dlouho.
Nalezněte takový rozvrh, ve kterém všechny lekce proběhnou v nejkratším čase a zároveň umožněte, aby se nepřekrývaly hodiny h1 a h2; h1 a h4; h3 a h5; h2 a h6; h4 a h5; h5 a h6; h1 a h6.
Řešení
Nejjednodušším řešením by bylo všechny hodiny seřadit za sebou - zajistili bychom tak, že každý, kdo si vybral hodinu h1, může jít i na hodinu h2 či jakoukoliv jinou (a tím bychom snadno splnili všechny podmínky ze zadání).
Úkolem je ale umožnit souběh hodin, u kterých nejsou studenti, kteří by měli zájem jít na obě hodiny současně.
Všechny hodiny zakreslíme jako vrcholy grafu. Hrany mezi nimi (které jsou neorientované) spojí vrcholy odpovídající hodinám, které nemají probíhat zároveň.
Zakreslujeme relaci "nemá probíhat zároveň" na množině hodin h1 až h6.
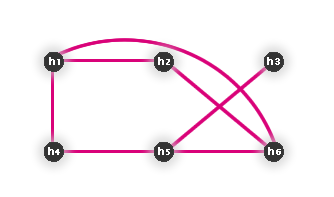
Obr. č. 3.21 - Graf popisující požadavky na rozvrh
Jednotlivým vrcholům budeme přiřazovat čísla (již v úloze barvení mapy jsme si ukázali, že přiřazování barev odpovídá přiřazování čísel).
Tato čísla budou odpovídat pořadí hodin v rozvrhu (pokud dvě hodiny dostanou číslo 1, budou v rozvrhu probíhat zároveň).
Při číslování budeme používat podobnou podmínku jako u sousedních států při barvení mapy - pokud dvě hodiny nemají začínat ve stejnou chvíli, jejich čísla budou různá.
Postup přiřazení hodin
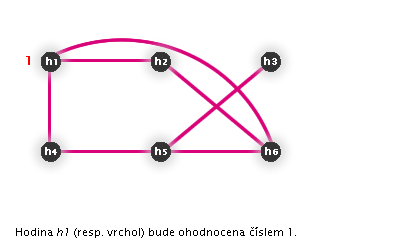
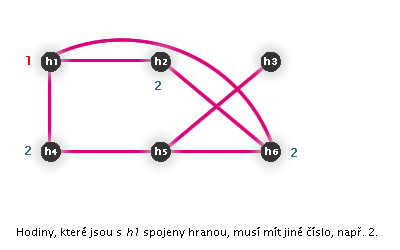
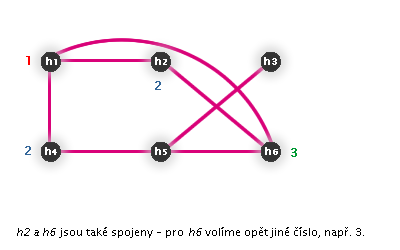
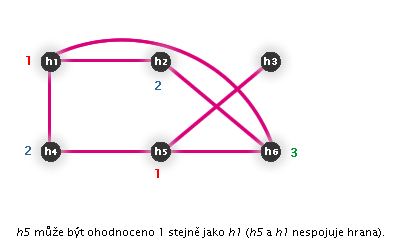
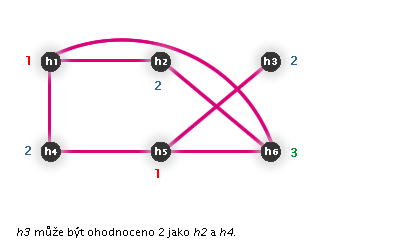

Závěr
Hledaný rozvrh hodin vyčteme z obarvení vrcholů grafu - vrcholy se stejnou barvou představují hodiny probíhající souběžně.
| 1. | 2. | 3. |
| h1 a h5 | h2, h3, h4 | h6 |
Minimální počet hodin, během kterých je možné odučit h1 až h6 za předepsaných podmínek, je 3.