3. Vybrané problémy / Teorie her
Úvod
Teorie her je oblast vědy, která zasahuje do více oborů (matematiky, psychologie, sociologie, ekonomie...) a zkoumá chování jednotlivých subjektů v okamžicích, při kterých dochází ke střetům zájmů. Můžeme sem řadit jak jednodušší hry (piškvorky, dáma), tak i složité ekonomické modely nebo například tzv. vězňovo dilema, které je příkladem spíše psychologie než matematiky v teorii her.
My se budeme věnovat té skupině her, kde snadno rozpoznáme, který hráč vyhrál a kde si můžeme hru rozdělit na jednotlivé tahy - vrstvy.
Příkladem nám mohou být piškvorky (3×3) - pravděpodobně jste zjistili, že hráč, který hru začne (a umístí svoji značku doprostřed mřížky), má mnohem větší naději na výhru - pokud neudělá chybu, nemůže prohrát.
Snadno si přitom můžeme rozkreslit možnosti, které nastávají - z prázdné mřížky vede 9 možností, kam umístí první hráč svoji značku, z každé další pak 8 možností atd. Někdy se nám hrany opět sbíhají (není důležité v jakém pořadí byly značky zakresleny), nikdy ale nevede možnost zpět (značku umazat).
Zde právě použijeme grafy: vrcholem zakreslíme aktuální stav hry (například popisem křížků a koleček vázajícím se ke konkrétnímu vrcholu) a orientovanou hranou možnost tahu.
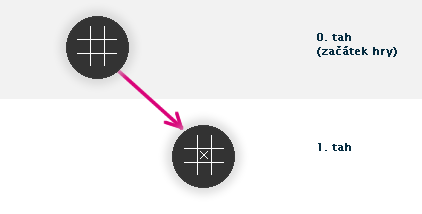
Obr. č. 3.31 - Příklad jednoho z možných tahů
Definice
Hra v explicitním tvaru je dána orientovaným acyklickým grafem G = (V, E) s vybraným vrcholem v0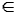 
V.
Na začátku vybere první hráč vrchol v 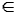V tak, že (v0, v) 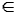E.
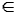Dále hráči střídavě vybírají vrcholy tak, že pokud vybral protihráč v posledním tahu vrchol u, musí hráč vybrat takový vrchol w, pro který (u, w) E.
Touto definicí jsme popsali způsob, jak mohou hráči táhnout. Jak ale zadefinovat vítěze hry?
Hráč, který již nemůže žádný vrchol vybrat, prohrál (tato definice je otázkou dohody mezi hráči).
Řekneme, že hráč má v této hře vyhrávající strategii, jestliže může volit tahy tak, že neprohraje, ať protihráč volí jakékoliv možné tahy.
Všimněte si, že mít vyhrávající strategii neznamená nutně vyhrát!
Například právě u piškvorek 3×3 má vyhrávající strategii první hráč. Pokud ale udělá chybu, může se stát, že vyhraje druhý hráč.
Pomocí teorie grafů můžeme u her v explicitním tvaru určit, kdo má vyhrávající strategii. Vzhledem k tomu, že zjistit všechny možnosti například pro šachy je stále technicky nemožné, nehrozí, že by naše vítězství určilo pořadí.
U jednodušších her (např. odebírání zápalek) to však možné je - příklad zde. Nejprve však potřebujeme rozhodující kritérium:
Uvažujme hru v explicitním tvaru určenou acyklickým orientovaným grafem G = (V, E) s vybraným vrcholem v0. Označme W jádro grafu G. Pak platí:
1. První hráč má vyhrávající strategii, jestliže v0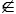 
W.
2. Druhý hráč má vyhrávající strategii, jestliže v0 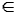W.
Nyní, známe-li vztah mezi jádrem grafu a vítězstvím ve hře, zkuste si znovu prohlédnout, jak se jádro v grafu hledá.
U některých her je nutné připustit i možnost remízy - můžeme ji například považovat za vítězství druhého hráče.