Teorie grafů

Snadno vidíme, že navážíme 1 kg, 2 kg, 5 kg a 8 kg (hmotnost všech závaží na jedné straně vah).
Otázkou zůstává, jaké jiné hmotnosti navážíme pomocí různého pokládání závaží na levou i pravou stranu vah.

Na každý vrchol grafu si zakreslíme dvě čísla - součet hmotností závaží na levé straně a součet hmotností na pravé straně.
Další vrcholy (= nové hmotnosti, které umíme navážit) budeme získávat přidáváním nových vrcholů tím, že ke stávajícím zkusíme přidat některé z dosud nepoužitých závaží.
Hrany budou znázorňovat přidání závaží na některou ze stran vah.

Každý vrchol v našem grafu bude znázorňovat jedno rozmístění závaží na vahách.

Dohodneme se, že předmět, jehož hmotnost hledáme, položíme na pravou misku vah - hmotnost závaží na levé straně přičítáme k hmotnosti tělesa, na pravé straně odečítáme.
Jak budou vypadat vrcholy grafu? Čísla odpovídající rozdílům (součet hmotností na levé straně)-(součet hmotností na pravé straně).
Jak budou vypadat hrany? Hrany popisují přidání závaží na některou ze stran. Zavedeme značení (+1 - přidání 1 kg závaží na levou stranu, -1 - přidání 1 kg závaží na pravou stranu).
Poznámka: může nastat situace, že stejná hmotnost je znázorněna více vrcholy (a nijak nám to nevadí, naopak vidíme více možností, jak se k dané hmotnosti dostat) - v obrázku však kreslíme jen jeden takový vrchol.
Například u 1 kg jsou dvě možnosti: 1 kg vlevo a vpravo hledaný předmět a nebo 2 kg vlevo a 1 kg vpravo (s předmětem).

Bude-li předmět vážit 3 kg - na levé straně máme 5 kg závaží, na pravé 2 kg závaží a hledaný předmět. Dvojice čísel, která tomuto stavu odpovídá, je (5,2).

Nyní máme popsáno, jak bude graf vypadat.

Začneme vrcholem (0,0) (prázdné váhy, resp. pouze předmět na pravé straně).

Budeme přidávat další vrcholy odpovídající přidávání závaží na váhy.

Dohoda: nebudeme přidávat závaží tak, aby vycházela hmotnost hledaného předmětu záporná (na pravé straně by spolu s předmětem byla závaží těžší než závaží na levé straně - váhy by se okamžitě převážily doprava a takový výsledek by neměl žádný význam, jen by znepřehledňoval graf).

Nejprve přidáme jedno závaží na levou stranu - dostáváme vrcholy (1,0) odpovídající 1 kg a obdobně (2,0) a (5,0).
Poté přidáme druhé závaží (vlevo či vpravo) - dostaneme např. 3 kg.
A obdobně pokračujeme dál.

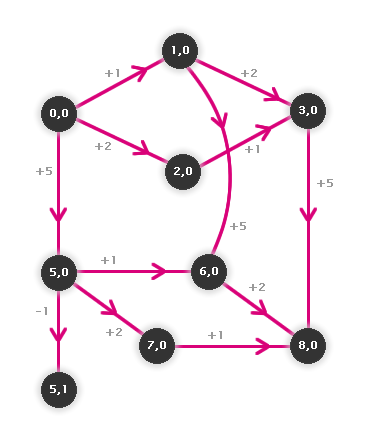
Na výsledném grafu nalezneme vrchol odpovídající každé z hmotností 1 kg-8 kg - tedy pokud hmotnost předmětu je jedna z těchto nalezených, dokážeme ji s pomocí rovnoramenných vah a závaží 5 kg, 2 kg a 1 kg zjistit.