3. Vybrané problémy / Relace
Úvod
Již v úvodu k teorii grafů jsme si popisovali grafy jako vhodný prostředek pro popis vztahů mezi konečným počtem objektů.
Použití grafů ke znázornění relací jsme si ukázali u příkladu s kamarády - zakreslovali jsme relaci "být kamarád s někým".
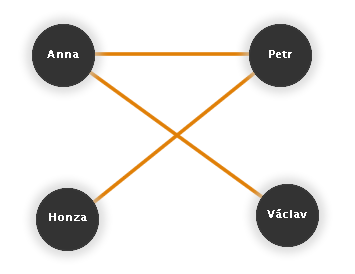
Příklad z Kapitoly 1: Úvod - 1.1
Podobně ale můžeme zakreslovat i jiné relace na jiných množinách představujících vrcholy grafu. Mohli bychom například na množině všech jednociferných přirozených čísel zakreslit relaci "je dělitelem" (přejít na příklad).
V celém textu budeme používat výraz "relace" ve významu "binární relace".
Matematická definice binární relace a definice vlastností (reflexivní...)
Kartézský součin
Nechť M a N jsou neprázdné množiny.
Kartézským součinem M×N rozumíme množinu všech uspořádaných dvojic:
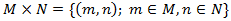
Relace
Relace je libovolná neprázdná podmnožina kartézského součinu.
(V našem případě používáme místo N opět M, uvažujeme kartézský součin mezi prvky stejné množiny - M×M.)
Značení: v následujících definicích budeme pro výraz "prvek m je v relaci s prvkem n" používat označení mRn.
Vlastnosti relací
Pro každé tři prvky m, n a o z množiny M platí:
(Řekneme, že relace na množině M je ..., jestliže pro každé tři prvky m, n a o z množiny M platí:)
Reflexivní: mRm
Symetrická: mRn → nRm
Antisymetrická (slabě): (mRn a zároveň nRm) → m = n
Antisymetrická (silně): Nikdy nenastane: mRn a zároveň nRm
Tranzitivní: (mRn a zároveň nRo) → mRo
(Podrobnější vysvětlení vlastnosti a ukázky, jak se projevují v grafu, následují. Zde jsou uvedeny pouze definice.)
Orientovaný nebo neorientovaný graf?
Ještě před začátkem kreslení grafu (nebo jiného řešení úlohy) je nutné si uvědomit, zda budeme používat orientované hrany nebo ne - vždy záleží na konkrétní úloze.
Například relace "znát se s někým" či "být kamarádem" jsou symetrické (viz níže), je tedy výhodnější použít jen jednu hranu. Naopak relace "je větší než", "je dělitelem" symetrické nejsou a ve znázornění situace je pro nás velmi důležité, jakým směrem vede hrana.
Také může nastat situace, že u jedné relace vedou některé hrany oběma směry a některé jen jedním směrem (relace "je větší nebo rovno než").
Shrnutí
1. Prvky zvolené množiny M znázorníme jako vrcholy budoucího grafu a vrcholy označíme stejně (případně vhodnými zkratkami) jako prvky M.
2. V grafu zakreslíme hranu AB právě tehdy, když je prvek A 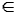 M v dané relaci k prvku B
M v dané relaci k prvku B 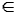 M.
M.
Jak se v grafu projevují vlastnosti relací (a jaký by to mělo praktický význam u relace "být kamarád" a "je dělitelem")?
Poznámka: vlastnosti relací uvažujeme u relací na kartézském množinu stejných množin (M×M) - tedy prvků ze stejné množiny.
- Reflexivní (= každý prvek je v relaci sám se sebou):
Z každého vrcholu vede hrana do něj zpět. Většinou pro nás tyto hrany nemají žádný význam a nemá smysl je do grafu zakreslovat.
Příklady:
Každý je kamarád sám se sebou.
Každé číslo je svým dělitelem.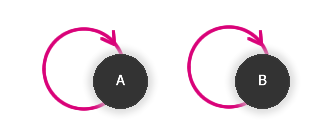
Obr. č. 3.12 - Ukázka reflexivní relace na množině M={A,B} - Symetrická (= je-li prvek A v relaci s B, pak je i B s A):
Používáme-li orientované hrany, povedou mezi každými dvěma vrcholy buď dvě šipky a nebo žádná šipka.
Pokud používáme neorientované hrany, chápeme každou hranu jako zakreslení symetrické relace (jako na obrázku 1.1).
Příklady:
Je-li A kamarádem s B, pak i B je kamarádem s A.
Je-li číslo x dělitelem y, pak je i y dělitelem x (tento výrok neplatí, relace "je dělitelem" není symetrická!).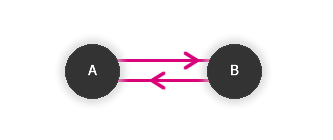
Obr. č. 3.13 - Ukázka symetrické relace na množině M={A,B} - Antisymetrická (= nenastává symetrie):
Antisymetrické relace dělíme na slabě antisymetrické a silně antisymetrické.
V případě slabě antisymetrické relace platí, že je-li A v relaci s B a B v relaci s A, pak A = B.
Nejde vždy nutně o opak symetrické relace - relace může být slabě antisymetrická i symetrická, například relace "rovná se".
Silně antisymetrická relace zakazuje všechny případy "A je v relaci s B a zároveň B s A." (tedy i možnost, že se prvky rovnají).
Příkladem je relace "je ostře menší než". - Tranzitivní (= je-li prvek A v relaci s B a B v relaci s C , pak je A v relaci s C):
Vede-li šipka z vrcholu A do B a (jiná) šipka z B do C, povede šipka i z A do C.
U neorientovaných grafů bude hranu znázorňovat úsečka místo šipky.
Příklady:
Je-li A kamarádem s B a B je kamarádem s C, pak i A je kamarádem s C ("přítel mého přítele je můj přítel").
Je-li 3 dělitelem 6 a 6 dělitelem 12, je 3 dělitelem 12.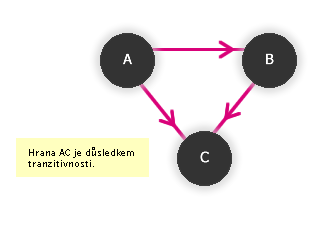
Obr. č. 3.14 - Ukázka tranzitivní relace na množině M={A,B,C}
Tyto tři vlastnosti (reflexivní, symetrická, tranzitivní) se mohou u jedné relace vyskytovat zároveň - je-li relace reflexivní, symetrická i tranzitivní, pak ji nazýváme ekvivalence.
Příkladem ekvivalence je relace "rovná se" na množině přirozených čísel či relace "je rovnoběžná s" na množině přímek v rovině.
Pokud je relace reflexivní, slabě antisymetrická a tranzitivní, nazýváme ji uspořádáním.
Příkladem je relace "je menší nebo rovno než" či relace "je dělitelem".
Pokud relace není reflexivní a je silně antisymetrická a tranzitivní, nazýváme ji ostrým uspořádáním.
Příkladem je relace "je menší než" na množině přirozených čísel.
Příklad č. 1 (dělitelé jednociferných čísel)
Zadání:
Zakreslete vztah "být dělitelem" na množině všech jednociferných přirozených čísel.
Řešení:
- 1) Vrcholy grafu budou jednotlivá čísla: 1, 2, 3, 4, 5, 6, 7, 8, 9.
- 2) Budou hrany grafu orientované nebo neorientované? (Bude relace symetrická?) - Relace nebude symetrická (to, že jedno číslo dělí druhé, neznamená, že druhé dělí první).
- 3) Všechny možné dvojice na dané množině zakreslíme do grafu - tzn. zakreslit z vrcholu 1 povede šipka do všech ostatních vrcholů (1 dělí všechna čísla), z vrcholu 2 do vrcholů 4, 6 a 8. Také bychom měli mít dalších 9 hran, protože každé číslo dělí samo sebe (z vrcholu 1 vede hrana do vrcholu 1, z vrcholu 2 do vrcholu 2 atd.). Tyto hrany ale nebudeme pro přehlednost zakreslovat. (Zakreslujeme jen tzv. vlastní dělitele.)
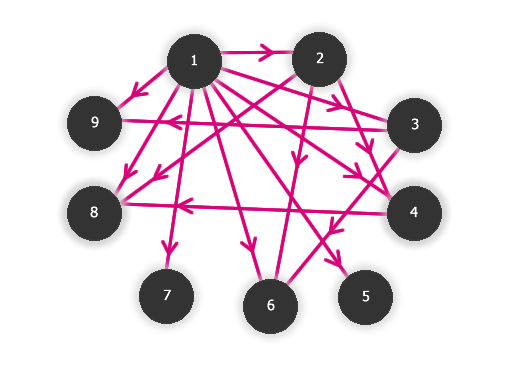
Obr. č. 3.15 - Výsledný graf úlohy na relaci dělitelnosti
Příklad č. 2 (kamarádi ze studií) [15]
Zadání:
Na nové škole se sešel mladý učitelský sbor. Nahraďme jména učitelů písmeny a do závorky udejme jejich věk:
A(32), B(24), D(25), E(35), H(34), K(26), L(33), M(28), P(29).
Dva učitelé se navzájem znali ze studií právě tehdy, když se jejich věk liší o méně než čtyři roky (předpokládáme, že všichni studovali stejnou školu).
Zakreslete graf relace "učitel A zná učitele B" definované na uvedené množině (učitelském sboru).
Řešení:
- 1) Vrcholy grafu budou představovat jednotlivé učitele.
- 2) Budou hrany orientované nebo neorientované? - Neorientované - jde o typický případ symetrického vztahu (když A zná B, pak zná i B osobu A).
- 3) U každé dvojice učitelů zkontrolujeme jejich věk a pokud se liší o méně než čtyři roky, zakreslíme hranu.
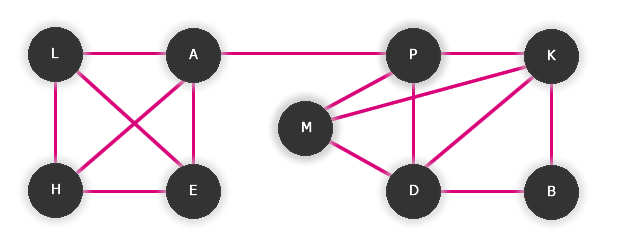
Obr. č. 3.16 - Výsledný graf daného učitelského sboru
Další využití relací najdeme také v řešení logických úloh - více informací naleznete v kapitole "Výroky".