2. Základní pojmy / Matematická definice grafu
Definice
Jak už bylo naznačeno v úvodu, grafy jsou vhodným prostředkem pro popis situací, které lze znázornit pomocí konečného množství bodů a vztahů mezi nimi znázornění pomocí hran.
Samotný graf G je definován jako dvojice dvou množin - vrcholů (V) a hran (E).
Někdy místo dvojice mluvíme o uspořádané dvojici (V,E) - myslí se tím, že na prvním místě jsou uvedeny vrcholy a na druhém hrany. Zkratky V a E pocházejí z angličtiny - vrcholy jsou anglicky VERTICES, hrany EDGES.
G = (V,E)
V dalších definicích používáme označení V(G) a E(G) pro množinu vrcholů V (resp. množinu hran E) grafu G.
Značení
V ... množina vrcholů
|V| ... velikost množiny vrcholů, tedy počet vrcholů (číslo)
E ... množina hran
|E| ... velikost množiny hran, tedy počet hran (číslo)
Důsledky
Množina hran E je podmnožinou množiny všech možných dvojic navzájem různých vrcholů - nepřipoušíme tedy "násobné" hrany ani "smyčky".
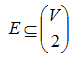
Poznámka
V této práci se budeme zabývat grafy, kde jsou každé dva vrcholy spojené nanejvýš jednou hranou. V případě, že jsou dva vrcholy spojené větším množstvím hran, hovoříme o takzvaných násobných hranách. Takovým grafům pak říkáme multigrafy.
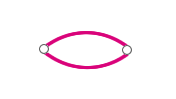
Obr. č. 2.1 - Příklad násobných hran
Podobně také nebudeme připouštět grafy obsahující smyčky - hrany spojující jeden vrchol sám se sebou.
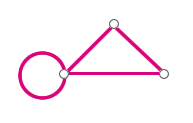
Obr. č. 2.2 - Příklad smyčky v grafu