3. Vybrané problémy / Toky v sítích
Úvod
Pomocí grafů můžeme řešit problém nalezení maximálního toku v síti.
Nejtypičtějším příkladem tohoto problému je vodovodní potrubí - zjišťujeme, kolik vody může potrubím protéct.
Pozor: maximálním tokem nerozumíme nějakou konkrétní část grafu ("nejširší potrubí"). Maximální tok je výsledek (číslo, viz níže) platný pro celý graf.
Do budoucna budeme v textu používat příklad s vodovodním potrubím. Mohli bychom ale uvažovat také silniční či datovou síť.
Co pro řešení takového problému potřebujeme znát?
- Popis potrubí - pro popis potrubí (kde jsou uzly, kolik je trubek...) použijeme orientovaný graf.
- Odkud voda teče - vrchol grafu, ze kterého vytéká do potrubí voda, který označíme jako zdroj s (s
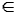 V, s z anglického source).
V, s z anglického source). - Kam voda teče - vrchol, který označíme jako stok (cíl, spotřebič) t (stok je některý z vrcholů grafu: t
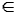 V, z anglického target).
V, z anglického target). - Kolik vody může daným místem (hranou) sítě protéct - budeme používat funkci kapacita.
- Kolik vody daným místem (hranou) opravdu protéká - znázorníme pomocí funkce tok.
Zdrojů i stoků může být v grafu obecně více, my však v dalším textu budeme předpokládat vždy jen jeden zdroj a jeden stok.
Vnitřními vrcholy budeme rozumět všechny vrcholy grafu kromě zdroje a stoku.
U silniční sítě by tedy kapacita odpovídala například množství aut, která mohou projet daným úsekem silnice za jednotku času (minutu). U datové sítě by to byla například přenosová rychlost. (Záměrně bychom neuvažovali o jednotlivých autech či datových paketech.)
Kapacita
Kapacita je funkce c přiřazující každé hraně nezáporné reálné číslo (c : E → R0+).
Podle definice může být kapacita nulová, v praxi se to však nepoužívá - stejný výsledek by nastal, kdyby taková hrana v grafu nebyla.
Poznámka
Přidáním opačné hrany s nulovou kapacitou můžeme dosáhnout symetričnosti hran.
Neplatí však obecně, že c(uv) = c(vu).
Tok
Tok je funkce f přiřazující každé hraně nezáporné reálné číslo. (f : E → R0+).
Definici vyhovuje i nulový tok.
Pro každou hranu e platí, že tok danou hranou nemůže být větší než je kapacita této hrany.
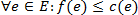
Tok také musí splňovat Kirchhoffův zákon:
Pro všechny vrcholy kromě zdroje a stoku platí, že součet toků na hranách vstupujících do vrcholu se musí rovnat součtu toků na hranách vycházejících z vrcholu.
Velikost toku (v celém grafu) získáme jako součet toků ze zdroje.
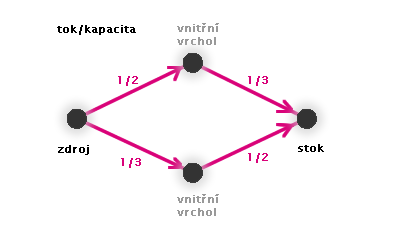
Obr. č. 3.25 - Příklad toku v síti (ne maximálního)
Jak jsme uvedli v definici, kapacita i tok mohou být reálná nezáporná čísla - v dalším textu však budeme předpokládat, že kapacity i toky jsou popsány přirozenými čísly.
Síť
Výše uvedené definice lze shrnout do následující definice sítě.
Síť je uspořádaná pětice (V, E, z, s, c), kde platí:
- (V, E) je orientovaný graf
- c: E → R0+ je kapacita hran
- z, s 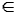 V jsou dva vrcholy grafu, kterým říkáme zdroj a stok
V jsou dva vrcholy grafu, kterým říkáme zdroj a stok
- graf je symetrický, tedy pro každé dva vrcholy u, v 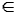 V: uv
V: uv 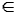 E právě tehdy, když vu
E právě tehdy, když vu 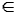 E. Pokud ale tyto hrany mají nulový tok, tak je do grafu nezakreslujeme (viz algoritmus).
E. Pokud ale tyto hrany mají nulový tok, tak je do grafu nezakreslujeme (viz algoritmus).
Přítokem rozumíme součet toků hran směřujících do vrcholu.
Odtokem chápeme součet toků hran vycházejících z vrcholu.
Ve zdroji nesmí být větší přítok než odtok.
Ve stoku naopak nesmí být odtok větší než přítok.
Primitivní algoritmus
Asi nejjednodušší možnost, která nás při hledání maximálního možného toku v síti napadne, je zkoušet všechny cesty ze zdroje do stoku a zkoumat, zda nemůžeme zvýšit tok, případně o kolik (není-li v grafu žádný tok, začneme zvyšováním nulového).
Na ukázkovém příkladě (obrázek 3.25, v1 je zdroj, v4 je stok) by to znamenalo prozkoumat dvě cesty - (v1, v3, v4) a (v1, v2, v4).
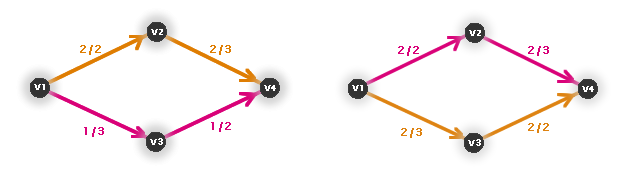
Obr. č. 3.26 - Příklad primitivního algoritmu
Dostali jsme maximální tok 4, což je správný výsledek.
U některých grafů ovšem může dojít k situaci, kdy nám tento postup vrátí špatný výsledek, viz obrázek č. 3.27 (na hranách jsou uvedeny jen kapacity, tok na začátku předpokládáme nulový, v1 je zdroj, v4 spotřebič).
Výsledek záleží na pořadí, ve kterém cesty zkoušíme.
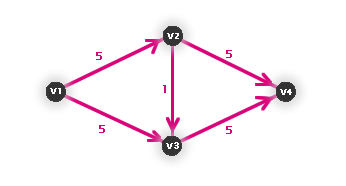
Obr. č. 3.27 - Příklad, kdy primitivní algoritmus selže (zadání)
Správný výsledek je zřejmě 10 (obrázek 3.28).
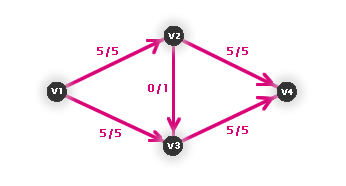
Obr. č. 3.28 - Příklad, kdy primitivní algoritmus selže (správný výsledek)
Pokud bychom ale začali zvyšovat tok nejprve na cestě (v1, v2, v3, v4), vyjde nám maximální tok v grafu jen 9.
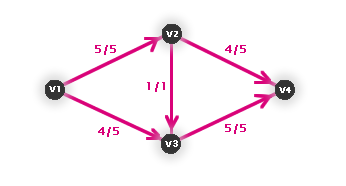
Obr. č. 3.29 - Příklad, kdy primitivní algoritmus selže (špatný výsledek)
Z toho důvodu zavádíme možnost, že po hraně pošleme tok opačným směrem. (To můžeme díky tomu, že síť je symetrická.)
Rezerva hrany
Rezerva hrany nám popisuje, jaká část kapacity na hraně zbývá - kolik vody by ještě mohlo v trubce protékat, kolik dalších aut by mohlo danou komunikací projíždět apod.
Zároveň také započítává zmiňovaný tok v opačném směru - s opačným znaménkem než původní tok.
Rezerva hrany uv: r(uv) = c(uv) - f(uv) + f(vu).
Ford-Fulkersonův algoritmus
Ford-Fulkersonův algoritmus také zkouší všechny cesty v grafu a hledá zlepšující tok, využívá přitom ale rezervy hrany.
Pro každou cestu, kde lze zvýšit tok, určí hodnotu  , o kterou bude tok zvyšovat.
, o kterou bude tok zvyšovat.
Pro každou hranu na cestě určí také hodnotu 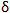 , která bude počítat, o kolik snížit tok proti směru hrany.
, která bude počítat, o kolik snížit tok proti směru hrany.
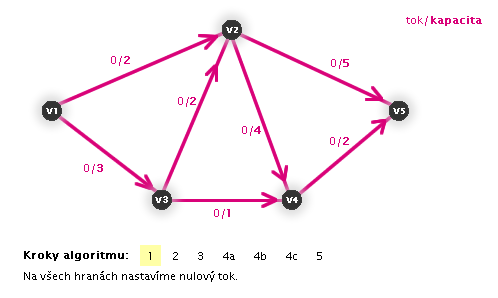
- 1. Na začátku mějme libovolný tok (může být všude nulový,
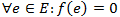 ).
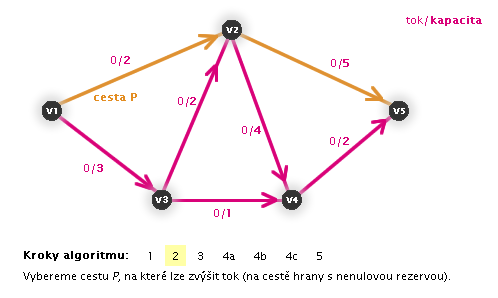
). - 2. Dokud existuje nějaká cesta P z vrcholu z do s taková, že každá hrana na cestě má nenulovou rezervu,
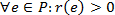 , vybereme ji.
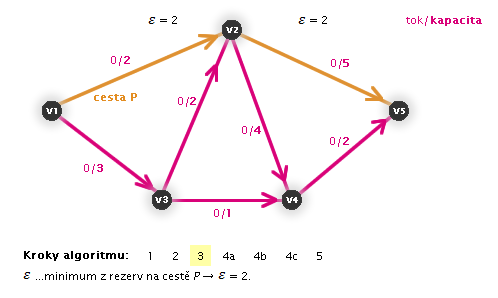
, vybereme ji. - 3. Zvolíme nejmenší rezervu z hran po cestě a její hodnotu si zapamatujeme jako
 .
. 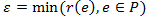
- 4. Pro všechny hrany na cestě (každou hranu vždy v tomto kroku pojmenujeme uv), uv
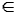 P:
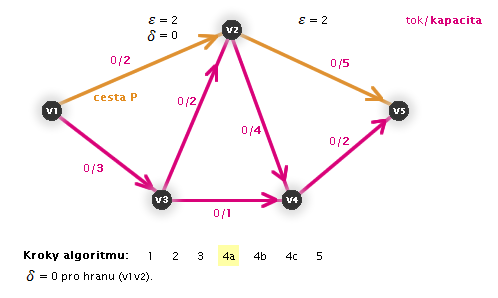
P: - 4a.
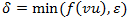 .
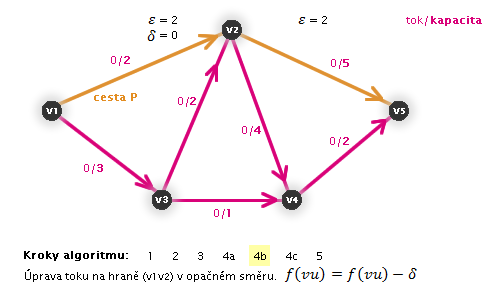
. - 4b. Upravíme tok na hraně (opačným směrem - f(vu)).
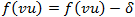 .
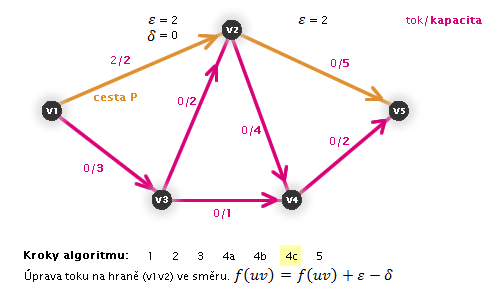
. - 4c. Upravíme tok na hraně (směrem f(uv)).
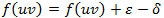 .
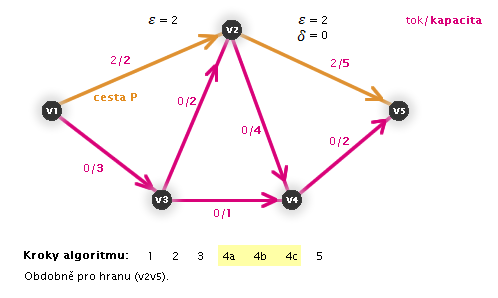
. - 5. Vyčerpáme-li všechny cesty, na kterých můžeme zlepšit tok, prohlásíme součet f (toků ze zdroje) za maximální tok.
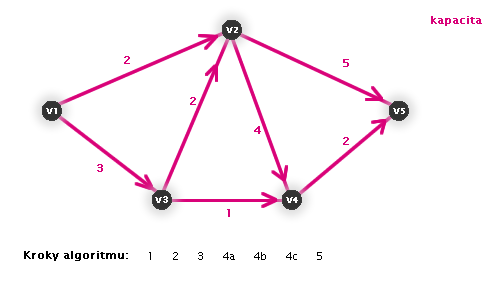
V následujících animacích uvidíte vždy aktuální krok zvýrazněný číslem:

Práce algoritmu (animace, zdroj: v1, stok: v5)
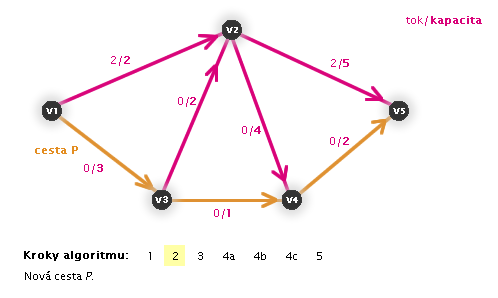
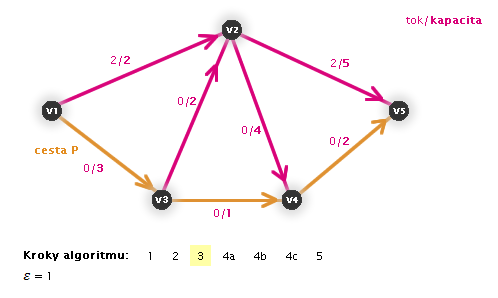
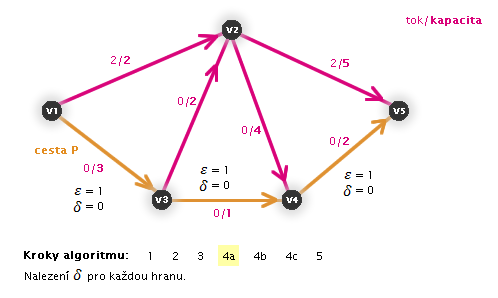
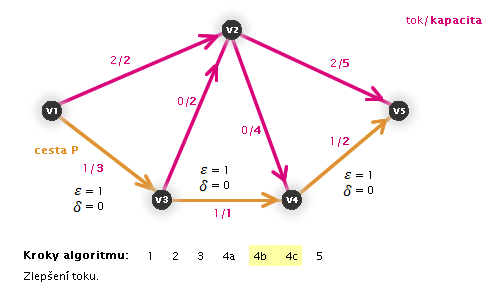
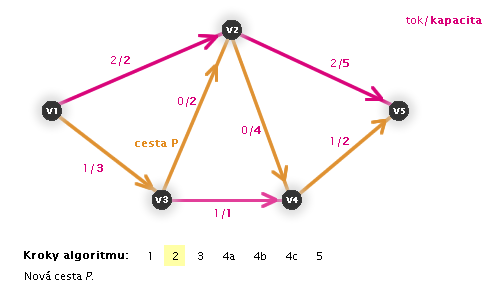
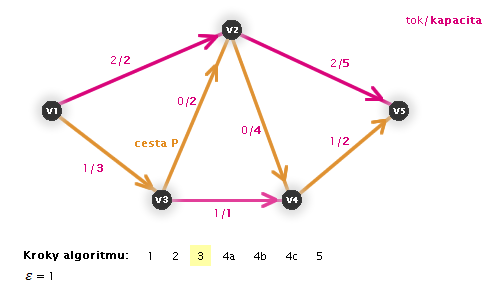
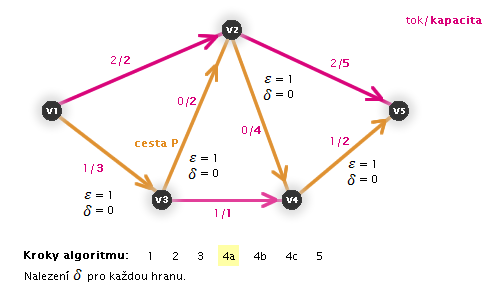
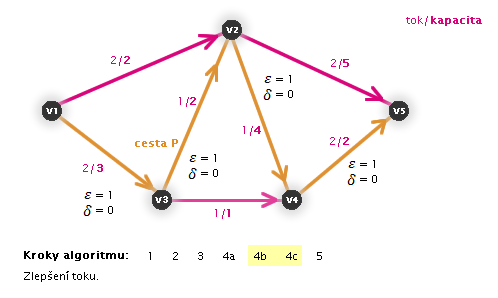
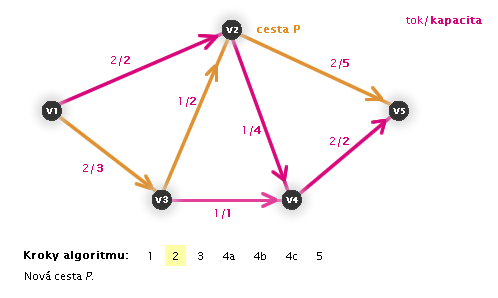
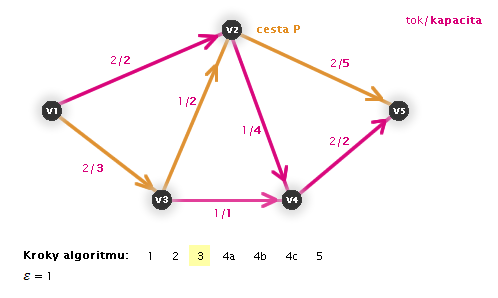
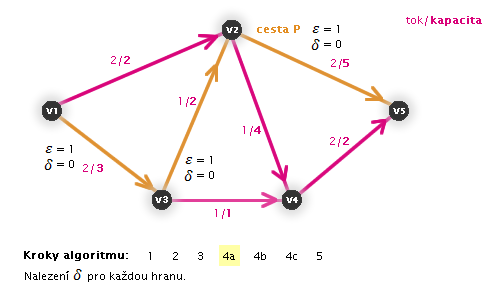
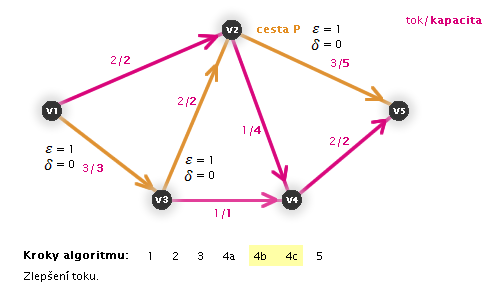
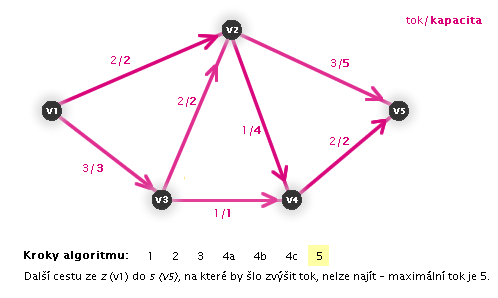

Zastaví se algoritmus?
Ano, v každém kroku totiž zvýší velikost toku alespoň o 1.
Najde algoritmus vždy maximální tok?
Pro důkaz pravdivosti tohoto tvrzení je potřeba zavést pojem řez, který v této práci vysvětlovat nebudeme - podrobnější informace naleznete v literatuře: [19]
Je výsledek jednoznačný?
Samotný maximální tok (číslo) jednoznačný je.
Můžeme se k němu ale dostat více způsoby. Rozmyslete si, jaké by byly možnosti u následujícího grafu (v1 zdroj, v6 stok).
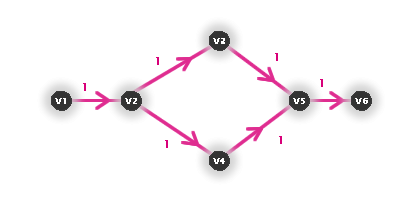
Obr. č. 3.30 - Graf s více možnostmi, jak dosáhnout maximálního toku
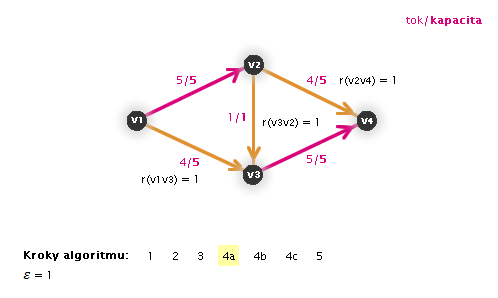
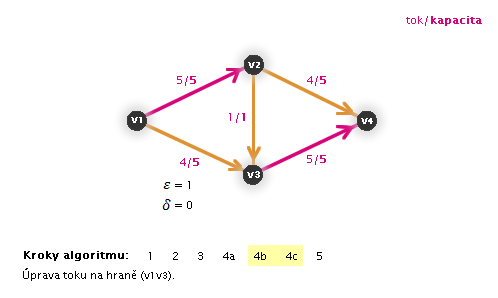
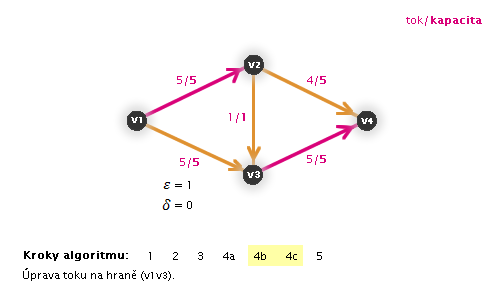
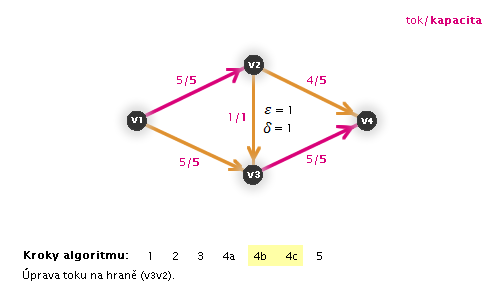
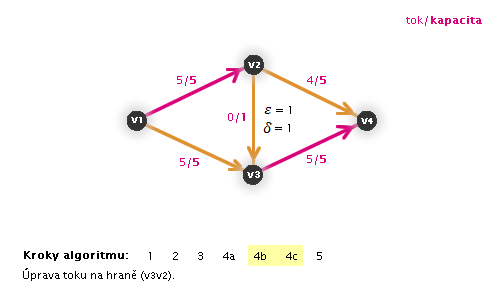
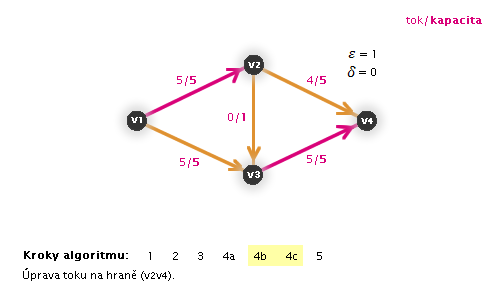
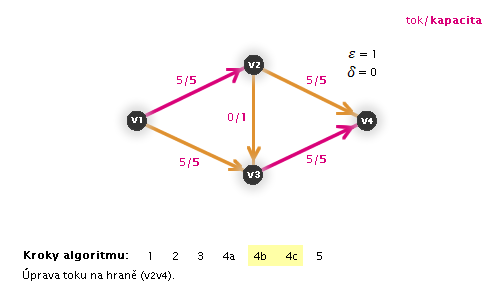
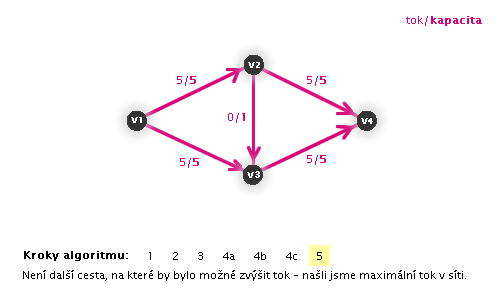
Příklad na obrázku 3.29
Díky tomu, že Ford-Fulkersonův algoritmus pracuje, dokud nenajde maximální tok, můžeme ho spustit již na grafu s tokem, kterým původně zamýšlený primitivní algoritmus skončil výpočet (proto následující animace již nezačíná krokem 1).
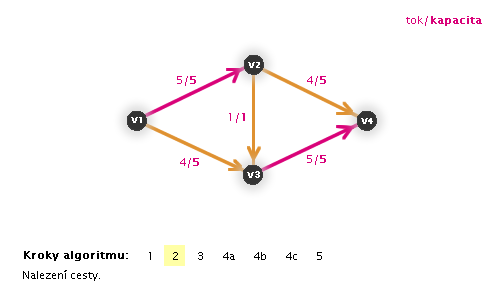
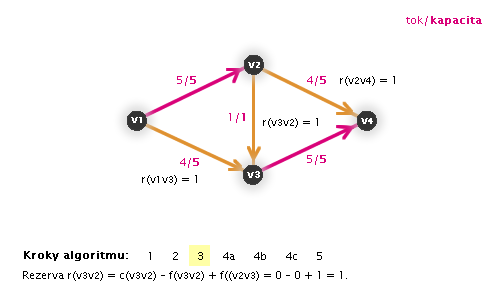

Jiné algoritmy na hledání maximálního toku
Další algoritmy na hledání maximální toku jsou například Dinitzův algoritmus nebo Edmonds-Karpův - jejich výhodou je nižší výpočetní složitost (= počet kroků algoritmu), jsou ovšem náročnější na implementaci. Více informací v [19].