2. Základní pojmy / Matematická reprezentace grafu
Dosud jsme všechny grafy popisovali pomocí obrázků. Často ale potřebujeme graf zadat pomocí čísel, například pro výpočty na počítači.
Matice sousednosti
Nejtypičtějším zápisem grafu je zápis pomocí matice.
Co je to matice?
Matice je matematické schéma, pomocí kterého se zapisují čísla (nebo jiné objekty) do obdélníkového tvaru.
Matice se používají v algebře pro studium různých objektů nebo pro řešení soustav rovnic. Pro účely teorie grafů nám postačí představit si matici jako tabulku čísel, kterou uzavřeme do závorek.
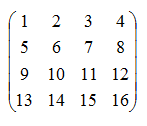
Obr. č. 2.18 - Příklad obecné matice
Často potřebujeme čísla z matice číst (nebo zapisovat) pomocí určení pozice prvku dvojicí (řádek, sloupec). Například na obr. 2.18 by číslo 10 bylo na pozici (3,2).
V této části se budeme zabývat neorientovanými grafy - zápis orientovaných grafů je popsán zde.
Postup vytváření matice sousednosti
- Nejprve si všechny vrcholy očíslujeme.
- Za rozměr matice musíme zvolit počet vrcholů. Kdybychom měli například graf se 4 vrcholy ale matici rozměrů jen 3×3, nemohli bychom zapsat hrany vedoucí do/z čtvrtého vrcholu.
- Pokud vede mezi dvěma vrcholy hrana, zapíšeme do matice na pozici [číslo jednoho vrcholu, číslo druhého vrcholu] a na pozici [číslo druhého vrcholu, číslo prvního vrcholu] číslo 1. Jinak zapíšeme 0.
Definice
Nechť G=(V,E) je graf s n vrcholy. Označme vrcholy v1,...,vn (v nějakém libovolném pořadí). Matice sousednosti grafu G je čtvercová matice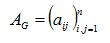 
definovaná předpisem:
Příklad
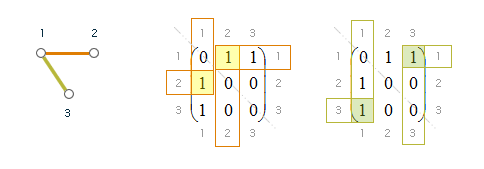
Obr. č. 2.19 - Příklad zápisu grafu pomocí matice sousednosti
Poznámka
Pro neorientované grafy platí, že jejich matice sousednosti jsou symetrické.
Pokud je graf G úplný, obsahuje matice AG s výjimkou hlavní diagonály samé jedničky.
Příklady
Obr. č. 2.20 - Graf a jeho matice sousednosti sousednosti
Obr. č. 2.21 - Graf a jeho matice sousednosti sousednosti
Obr. č. 2.22 - Úplný graf a jeho matice sousednosti sousednosti
Jiné možnosti reprezentace grafu
Kromě matice sousednosti je možné použít i jiné reprezentace - pokud bude mít hodně vrcholů, které budou spojeny relativně malým počtem hran mezi nimi, je výhodnější použít například seznam sousedů či seznam vrcholů se seznamem hran.
Obr. č. 2.23 - Příklad zápisu grafu pomocí seznamů vrcholů a hran