3. Vybrané problémy / Maximální kostra grafu
Úvod
V případě kostry grafu jsme zvyklí většinou hledat minimální kostru, užitečné výsledky nám ale často přináší i maximální kostra = souvislý podgraf (typu strom) s celkovým maximálním ohodnocením hran. Pro zjednodušení budeme uvažovat pouze souvislé neorientované grafy (neorientované proto, aby nenastalo různé ohodnocení hran AB a BA).
Předpokládejme, že máme graf, ve kterém vrcholy odpovídají prvkům z reálného světa (např. státy) a hrany jsou ohodnoceny dle nějakého ukazatele znázorňujícího podobnost vrcholů. Konkrétní význam ukazatele pro nás při hledání maximální kostry není podstatný. Typicky se jedná o číslo nabývající hodnoty 1, pokud se dva vrcholy v nějaké vlastnosti naprosto shodují, hodnoty 0, pokud se neshodují vůbec, či hodnoty mezi 0 a 1 (např: 0,5 - shoda v polovině případů). Často je takový graf úplný.
Příklady
- A: Vrcholy grafu odpovídají státům, hrany jsou ohodnoceny podle exportu (nebo importu) zboží mezi zeměmi. Čím vyšší je hodnota ukazatele, tím větší je pohyb zboží mezi těmito dvěma státy.
- B: Vrcholy grafu představují univerzity, ohodnocení hran odpovídá přechodům studentů mezi univerzitami.
- C: Vrcholy grafu znázorňují zboží v obchodech. Čím větší je hodnota ukazatele mezi dvěma typy zboží, tím častěji jsou kupována společně. Hodnota 1 představuje možnost, že zákazníci vždy kupují tyto dva druhy zboží spolu (v rámci všech objednávek), a hodnota 0, že naopak neexistuje žádná objednávka, na které by byly oba druhy spolu.
Význam maximální kostry grafu
Díky postupu, jakým maximální kostru najdeme (následuje), víme, že do maximální kostry použijeme vždy hrany s nejvyšším ohodnocením. Tím pospojujeme vrcholy, které k sobě "nejvíce patří".
V případě příkladu se státy (A) zapojujeme do maximální kostry dvojice států, které mezi sebou mají největší export/import.
Podobně u univerzit používáme takové, mezi kterými přecházejí studenti nejčastěji a u obchodů (C) zboží, které je nejčastěji objednáváno společně (podobně fungují nákupní rádci v internetových obchodech, které před potvrzením objednávky poradí, jestli nechcete k digitálnímu fotoaparátu paměťovou kartu).
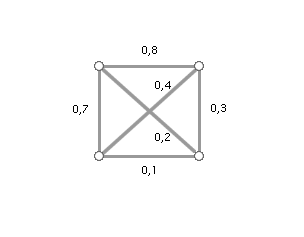
Obr. č. 3.11 - Příklad maximální kostry grafu (zadání)
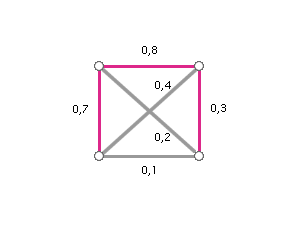
Obr. č. 3.12 - Příklad maximální kostry grafu (řešení)
Nalezení maximální kostry
Pokud známe postup, jak najít minimální kostru, je nalezení maximální kostry jednoduché - stačí ohodnocení hran změnit na opačné (kladné → záporné) hodnoty a použít libovolný algoritmus pro nalezení minimální kostry (a opět otočit znaménko ohodnocení hran).
Druhou možností je upravit samotný hladový algoritmus - např. Kruskalův. Hrany ale seřadíme nikoliv vzestupně, ale sestupně - nejprve do kostry přidáváme hrany s největším ohodnocením.