Teorie grafů

3. Vybrané problémy / Hra NIM (odebírání sirek)

Úvod

Na hře NIM (= odebírání sirek) si ukážeme praktické využití znalostí z oblasti teorie her - jak pomocí jádra grafu už před začátkem hry můžeme určit, který hráč má vyhrávající strategii - stačí nám k tomu pouze vědět, kdo začíná (a kolik hromádek sirek je ve hře).

Ve hře NIM hráči postupně odebírají sirky a ten, který odebere poslední sirku vyhrál/prohrál (záleží na variantě hry). My si popíšeme hru, ve které je více hromádek sirek a každý hráč může z jedné hromádky odebrat od jedné do všech sirek. Vítězem je pak hráč, který odebral poslední sirku (viz dále).
Poznámka: další častou variantou hry je jedna hromádka sirek, ze které hráči při každém tahu odebírají 1-3 sirky.

Popis hry

Uvažujme k hromádek sirek, kdy v i-té hromádce je n_i 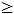1 sirek, i = 1,..., k. Hráči střídavě odebírají sirky z hromádek.
V daném tahu si hráč zvolí hromádku, z které bude odebírat (kde ještě nejsou odebrány všechny sirky) a odebere minimálně jednu a maximálně všechny sirky vybrané hromádky.
Hráč, který odebere poslední sirku, vyhrál.
Hru NIM s k hromádkami o n₁,...,n_k sirkách budeme značit NIM(n₁,...,n_k).

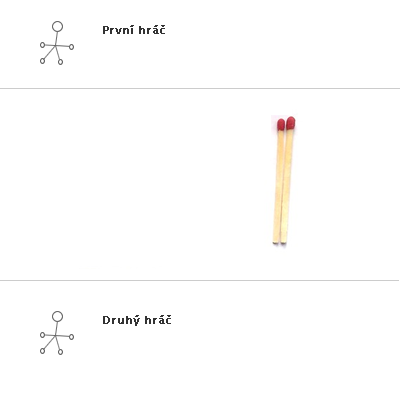
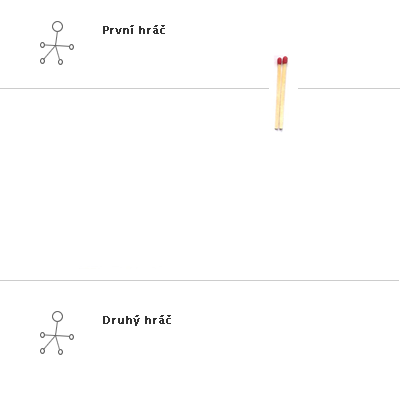
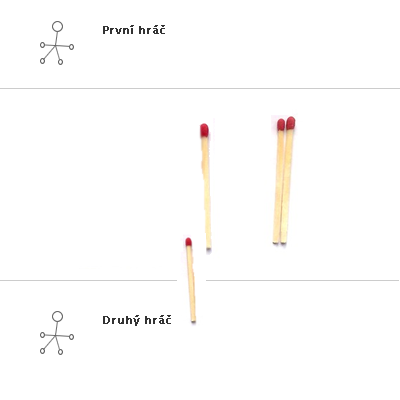
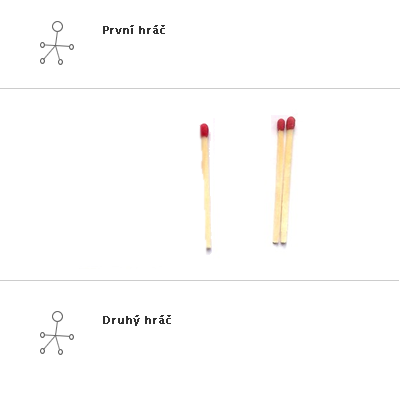
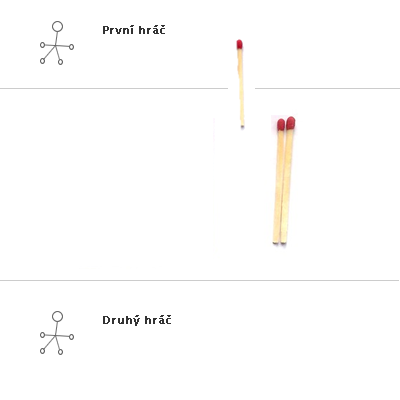
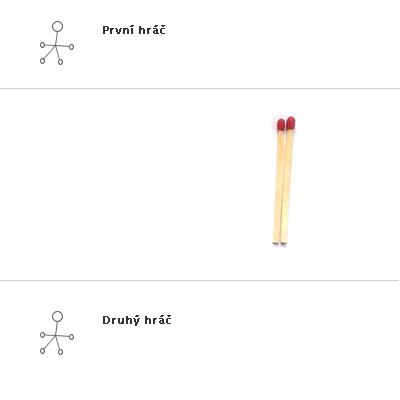
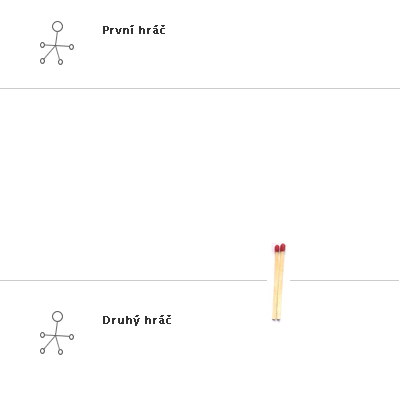
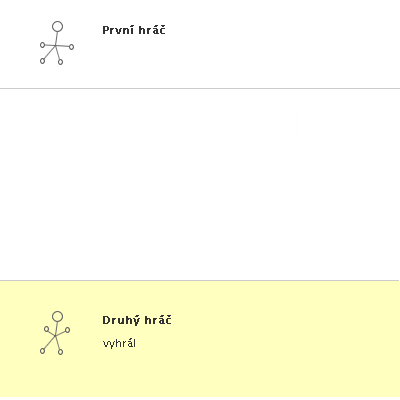
Obr. č. 3.32 - Příklad hry NIM(3,2,2)

Ukázka konkrétní hry s výhrou prvního hráče

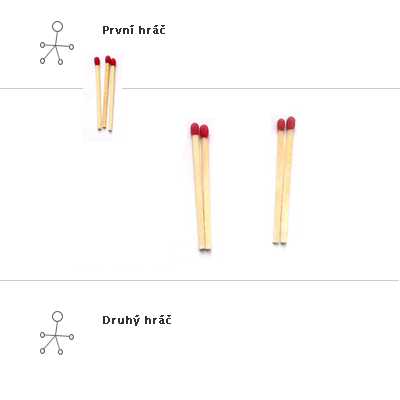
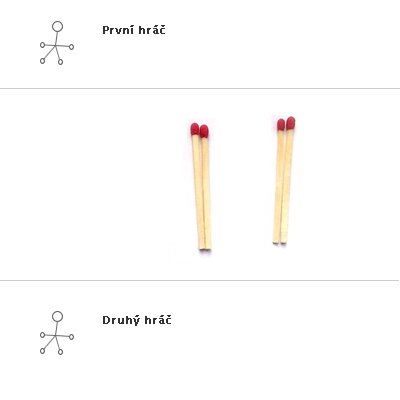
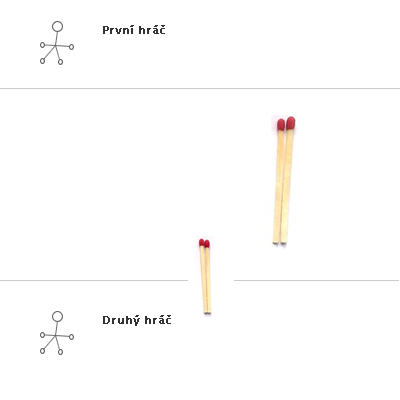
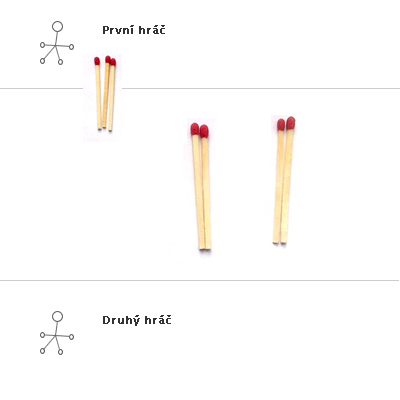
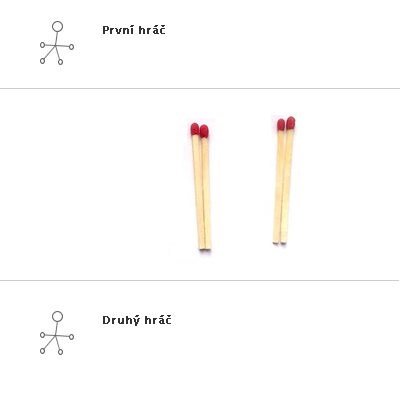
Stejná hra s výhrou druhého hráče

Jak využít teorii grafů?

Hru můžeme zakreslit pomocí grafu, viz následující obrázek. Rozsah grafu výrazně roste jak s množstvím hromádek, tak s množstvím sirek, proto jsme situaci zjednodušili na hru NIM(2,2).

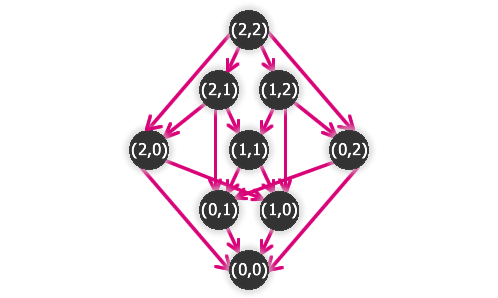
Obr. č. 3.33 - Hra NIM(2,2) zakreslená pomocí grafu

Co znamenají čísla u jednotlivých vrcholů?
Jak již bylo vidět na úvodním obrázku (3.32), počty sirek na jednotlivých hromádkách zapíšeme jako uspořádanou k-tici. Ta popisuje stav hry v dané chvíli a zapíšeme ji k vrcholu grafu. Hrana vedoucí do jiného vrcholu pak znamená, že je možný takovýto tah (viz obrázek 3.34).

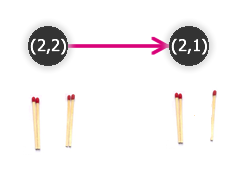
Obr. č. 3.34 - Význam čísel příslušných k vrcholům grafu

Například z vrcholu (2,2) vedou orientované hrany do čtyř vrcholů - (2,0), (2,1), (1,2), (0,2) - podle toho, odebereme-li jednu nebo dvě sirky a odebereme-li je z první nebo druhé hromádky.
Do některých vrcholů může vést také více cest (hlavně vždy vede cesta od vrcholu (2,2) do vrcholu (0,0) - ať hrajeme jakkoliv, nakonec oba hráči odeberou všechny sirky).

Možnost vývoje konkrétních her spolu se zakreslením do grafů

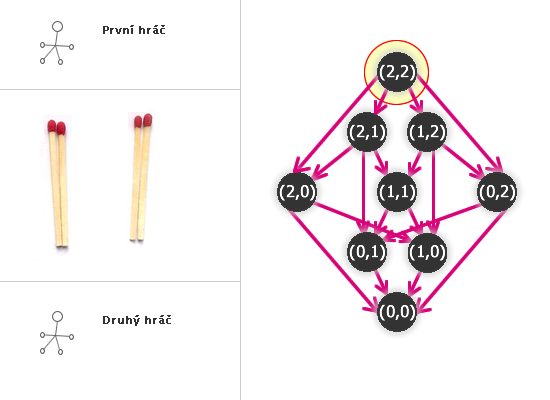
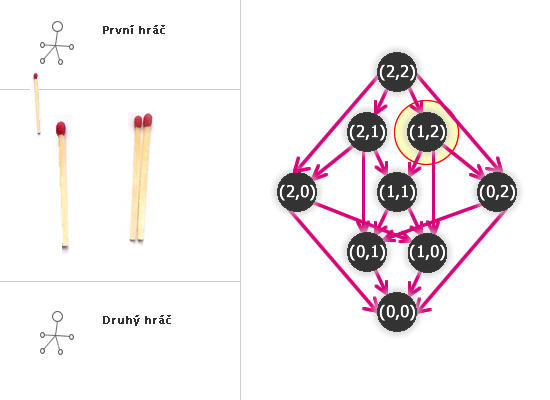
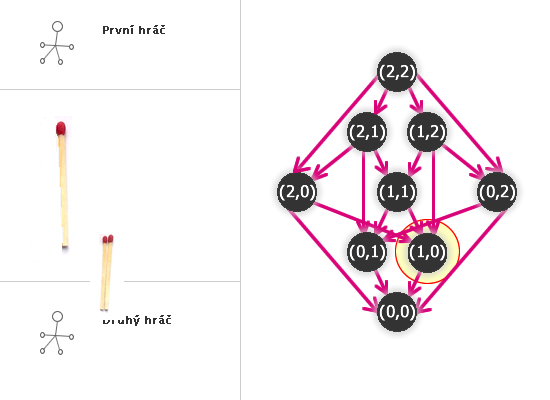
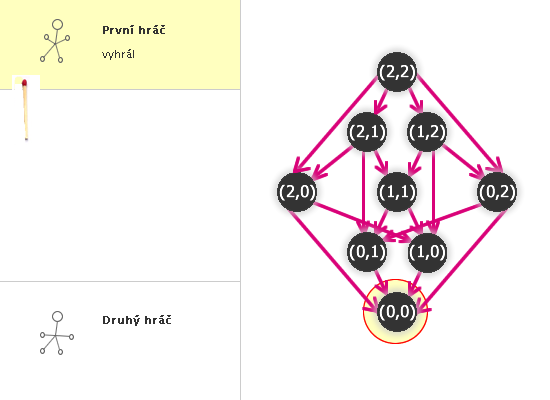
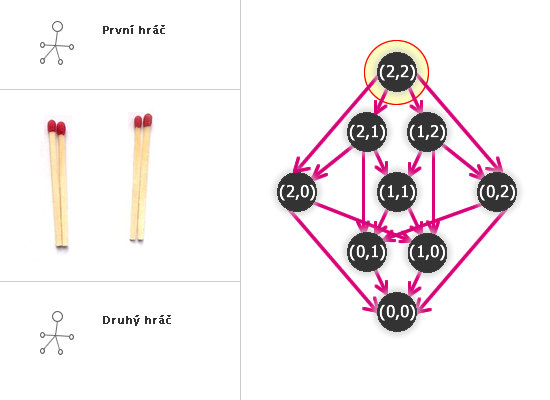
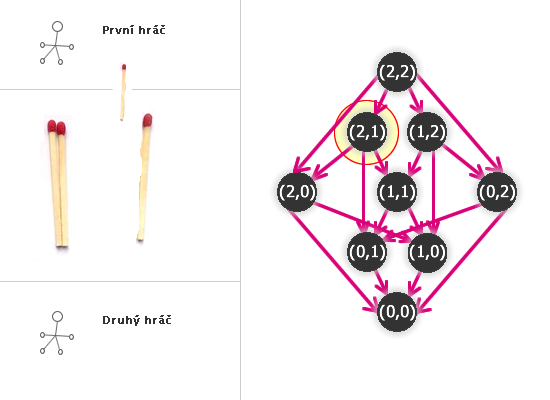
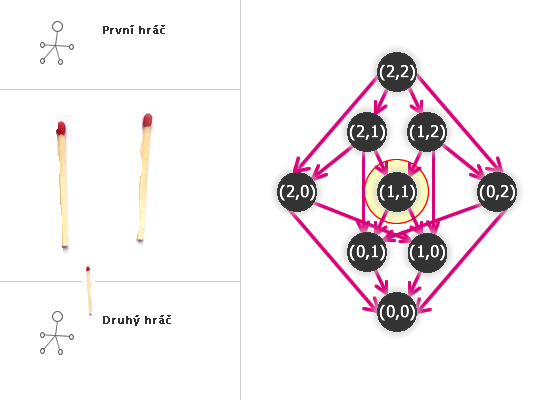
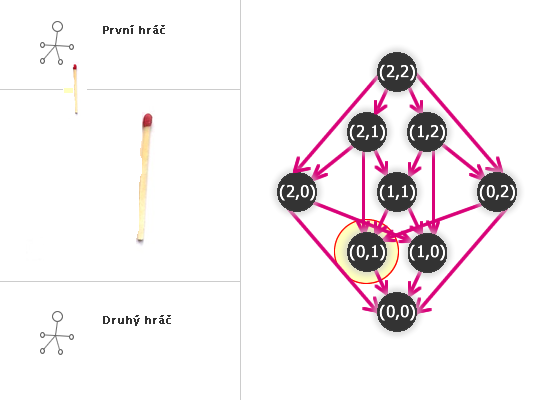
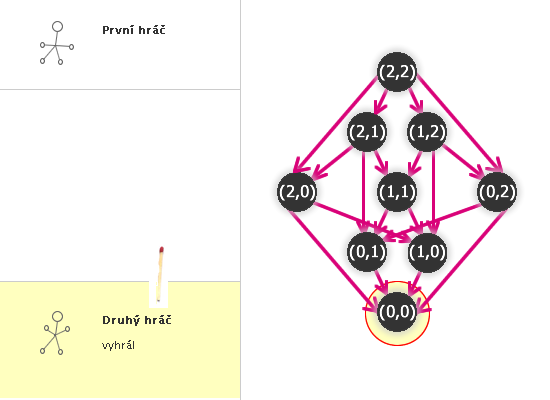
Kdo tedy vyhraje NIM(2,2)?

Nejprve zkusme úlohu vyřešit úvahou. První (začínající hráč) může odebrat jednu nebo dvě sirky.

Odebral jednu sirku:
(Hra tedy zůstala ve stavu (2,1) nebo (1,2), předpokládejme bez újmy na obecnosti (2,1).) Druhý hráč, chce-li vyhrát, musí odebrat také jednu sirku z první hromádky (tedy (1,1)). Prvnímu pak nezbyde nic jiného, než vzít jednu sirku (ať už z první nebo druhé hromádky) a druhý hráč odebere zbývající poslední a vyhrál.
Kdyby totiž druhý hráč vzal po prvním tahu obě dvě sirky z první hromádky ((0,1)), první vezme poslední zbývající a vyhrál.
A kdyby druhý hráč po prvním tahu vzal jednu z druhé hromádky ((2,0)), první vezme zbývající dvě a vyhrál.

Odebral dvě sirky:
Hra je v tom případě (2,0) nebo (0,2). Druhý hráč tedy odebere zbylé dvě sirky a vyhrál.

Vidíme tedy, že vyhrávající strategii má druhý hráč - neudělá-li chybu, neprohraje.
Podle této souvislosti mezi jádrem grafu a vyhrávající strategií by tedy v jádru grafu odpovídajícího dané hře měl být vrchol popisující začátek NIMu(2,2).

Pokud ke grafu na obrázku 3.33 nalezneme jeho jádro, dostaneme tento výsledek:

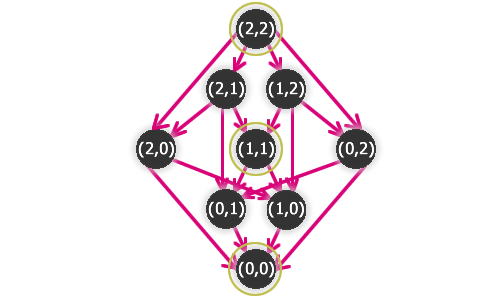
Obr. č. 3.35 - Graf hry NIM(2,2) s vyznačeným jádrem

Počáteční vrchol je obsažen v jádru grafu, odpovídá to tedy závěru, ke kterému jsme u tohoto příkladu došli úvahou.

Příklady na procvičování