Teorie grafů

2. Základní pojmy / Stromy

Definice

Strom je souvislý graf neobsahující kružnici.

Z definice stromu vyplývá, že mezi každými dvěma vrcholy existuje právě jedna cesta (alespoň jedna cesta, protože je souvislý; nemůže nastat situace více cest, protože díky neexistenci kružnice není možné zvolit "objížďku").

Obr. č. 2.29 - Příklady stromů

Eulerův vzorec (pro stromy)

Pro stromy také platí následující vztah mezi počty hran a vrcholů:

|V| = |E| + 1

Využití stromů v informatice

Stromy se často využívají pro ukládání dat (typicky čísel) v informatice jako tzv. datová struktura (zjednodušeně způsob uložení dat).

Takovou typickou datovou strukturou je binární vyhledávací strom.
Jde o strom, kde z každého vrcholu vedou nanejvýš tři hrany (jedna "seshora" - říkáme od "otce" - a maximálně dvě "dolů" - k dvěma "synům") a kde pro každý prvek platí, že jeho levý syn je menší nebo roven otci, pravý syn větší. Pojmy levý a pravý zde jsou jednoznačné, musí být splněna podmínka, že směrem vlevo je číslo menší nebo rovno, směrem vpravo je číslo větší.

Důvodem, proč se takové struktury používají, je např. rychlejší nalezení prvku, než kdyby byly všechny prvky "za sebou" (v poli, spojovém seznamu).

V tomto typu úloh se nepoužívá matice sousednosti, ale typicky dynamické datové struktury (ukazatelé + malloc (C), ukazatelé + new (Pascal)) - nechceme ukládat graf pomocí čísel, ale naopak čísla pomocí grafu.

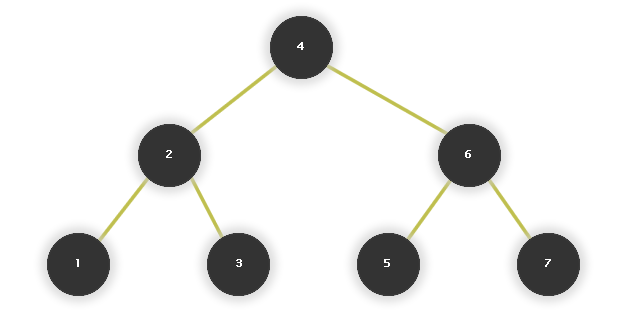
Obr. č. 2.30 - Binární vyhledávací strom